ツリーソート – 二分探索ツリーを使用したソート。時間計算量 – O(n²)。このようなツリーでは、左側の各ノードにはノードより小さい番号があり、右側にはノードより大きい番号があります。ルートから来て左から右に値を出力すると、ソートされた番号のリストが得られます。 。驚くべきことですね?
二分探索ツリー図を考えてみましょう。
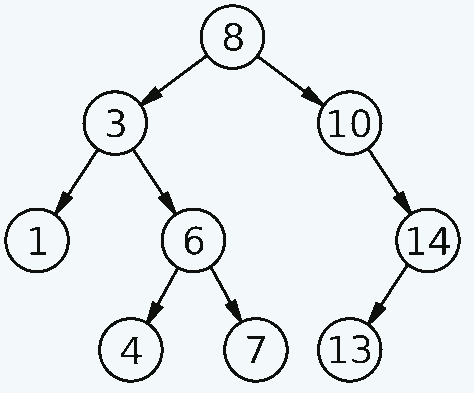
デリック・クッツェー (パブリック ドメイン)
左下の各ノード、つまり右側のノードごとに、左下隅の最後から 2 番目の左ノードから数字を手動で読み取ってみてください。
次のようになります:
<オル>
コードでアルゴリズムを実装するには、次の 2 つの関数が必要です。
<オル>
二分探索木は読み取られたときと同じ方法で組み立てられ、それが大きいか小さいかに応じて、左側または右側の各ノードに番号が付けられます。
Lua での例:
function Node:new(value, lhs, rhs)
output = {}
setmetatable(output, self)
self.__index = self
output.value = value
output.lhs = lhs
output.rhs = rhs
output.counter = 1
return output
end
function Node:Increment()
self.counter = self.counter + 1
end
function Node:Insert(value)
if self.lhs ~= nil and self.lhs.value > value then
self.lhs:Insert(value)
return
end
if self.rhs ~= nil and self.rhs.value < value then
self.rhs:Insert(value)
return
end
if self.value == value then
self:Increment()
return
elseif self.value > value then
if self.lhs == nil then
self.lhs = Node:new(value, nil, nil)
else
self.lhs:Insert(value)
end
return
else
if self.rhs == nil then
self.rhs = Node:new(value, nil, nil)
else
self.rhs:Insert(value)
end
return
end
end
function Node:InOrder(output)
if self.lhs ~= nil then
output = self.lhs:InOrder(output)
end
output = self:printSelf(output)
if self.rhs ~= nil then
output = self.rhs:InOrder(output)
end
return output
end
function Node:printSelf(output)
for i=0,self.counter-1 do
output = output .. tostring(self.value) .. " "
end
return output
end
function PrintArray(numbers)
output = ""
for i=0,#numbers do
output = output .. tostring(numbers[i]) .. " "
end
print(output)
end
function Treesort(numbers)
rootNode = Node:new(numbers[0], nil, nil)
for i=1,#numbers do
rootNode:Insert(numbers[i])
end
print(rootNode:InOrder(""))
end
numbersCount = 10
maxNumber = 9
numbers = {}
for i=0,numbersCount-1 do
numbers[i] = math.random(0, maxNumber)
end
PrintArray(numbers)
Treesort(numbers)Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/treesort
Источники
Convert Sorted Array to Binary Search Tree (LeetCode 108. Algorithm Explained) – YouTube
Sorting algorithms/Tree sort on a linked list – Rosetta Code
How to handle duplicates in Binary Search Tree? – GeeksforGeeks
Tree Sort | GeeksforGeeks – YouTube
バケットソート
バケット並べ替え – バケットごとに並べ替えます。このアルゴリズムはカウンティングソートに似ていますが、数値が「バケット」範囲に収集され、その後、他の十分に生産性の高いソートアルゴリズムを使用してバケットがソートされ、最後のステップで「バケット」の範囲が展開される点が異なります。 1 ずつ増やすと、ソートされたリストが得られます。
アルゴリズムの時間計算量は O(nk) です。このアルゴリズムは、一様分布の法則に従うデータに対して線形時間で機能します。簡単に言うと、要素は「スパイク」のない特定の範囲内にある必要があります (たとえば、0.0 から 1.0 までの数値)。そのような数字の中に 4 または 999 がある場合、中庭法によれば、そのような列は「偶数」とみなされなくなります。
Julia での実装例:
buckets = Vector{Vector{Int}}()
for i in 0:bucketsCount - 1
bucket = Vector{Int}()
push!(buckets, bucket)
end
maxNumber = maximum(numbers)
for i in 0:length(numbers) - 1
bucketIndex = 1 + Int(floor(bucketsCount * numbers[1 + i] / (maxNumber + 1)))
push!(buckets[bucketIndex], numbers[1 + i])
end
for i in 0:length(buckets) - 1
bucketIndex = 1 + i
buckets[bucketIndex] = sort(buckets[bucketIndex])
end
flat = [(buckets...)...]
print(flat, "\n")
end
numbersCount = 10
maxNumber = 10
numbers = rand(1:maxNumber, numbersCount)
print(numbers,"\n")
bucketsCount = 10
bucketSort(numbers, bucketsCount)На производительность алгоритма также влияет число ведер, для большего количества чисел лучше взять большее число ведер (Algorithms in a nutshell by George T. Heineman)
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/bucketSort
Источники
https://www.youtube.com/watch?v=VuXbEb5ywrU
https://www.youtube.com/watch?v=ELrhrrCjDOA
https://medium.com/karuna-sehgal/an-introduction-to-bucket-sort-62aa5325d124
https://www.geeksforgeeks.org/bucket-sort-2/
https://ru.wikipedia.org/wiki/%D0%91%D0%BB%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0
https://www.youtube.com/watch?v=LPrF9yEKTks
https://en.wikipedia.org/wiki/Bucket_sort
https://julialang.org/
https://www.oreilly.com/library/view/algorithms-in-a/9780596516246/ch04s08.html
基数ソート
基数ソート – 基数ソート。このアルゴリズムは、要素の比較がないという点でカウント ソートに似ています。代わりに、要素が *文字ごと* に *バケット* (バケット) にグループ化され、バケットは現在の数値文字のインデックスによって選択されます。時間計算量 – O(nd)。
次のように動作します:
- 入力は数字 6、12、44、9 になります
- リスト (0 ~ 9) のバケットを 10 個作成し、そこに少しずつ数字を追加/並べ替えます。
次へ:
<オル>
Scala での基数ソートの例:
import scala.util.Random.nextInt
object RadixSort {
def main(args: Array[String]) = {
var maxNumber = 200
var numbersCount = 30
var maxLength = maxNumber.toString.length() - 1
var referenceNumbers = LazyList.continually(nextInt(maxNumber + 1)).take(numbersCount).toList
var numbers = referenceNumbers
var buckets = List.fill(10)(ListBuffer[Int]())
for( i <- 0 to maxLength) { numbers.foreach( number => {
var numberString = number.toString
if (numberString.length() > i) {
var index = numberString.length() - i - 1
var character = numberString.charAt(index).toString
var characterInteger = character.toInt
buckets.apply(characterInteger) += number
}
else {
buckets.apply(0) += number
}
}
)
numbers = buckets.flatten
buckets.foreach(x => x.clear())
}
println(referenceNumbers)
println(numbers)
println(s"Validation result: ${numbers == referenceNumbers.sorted}")
}
}
このアルゴリズムには、GPU などで並列実行するためのバージョンもあります。ちょっとした並べ替えオプションもあります。これは非常に興味深く、本当に息をのむようなものに違いありません。
リンク
https://gitlab .com/demensdeum/algorithms/-/blob/master/sortAlgorithms/radixSort/radixSort.scala
ソース
https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8F%D 0%B4%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0% BA%D0%B0
https://www.geeksforgeeks.org/radix-sort/
https://www.youtube.com/watch?v=toAlAJKojos
https://github.com/gyatskov/radix-sort
ヒープソート
ヒープソート – ピラミッドソート。アルゴリズムの時間計算量 – O(n log n)、速いですよね?私はこれを、落ちてくる小石の選別と呼んでいます。これを説明する最も簡単な方法は視覚的に説明することだと思います。
入力は、次のような数値のリストです。
5、0、7、2、3、9、4
左から右に、データ構造、つまりバイナリ ツリー、または私がそれを呼んでいる – が作成されます。ピラミッド。ピラミッド要素には最大 2 つの子要素を含めることができますが、最上位の要素は 1 つだけです。
バイナリ ツリーを作成しましょう:
⠀⠀5
⠀0⠀7
2 3 9 4
ピラミッドを長い間見てみると、これらは配列からの単なる数値であり、次々に来て、各フロアの要素の数が 2 倍になっていることがわかります。
次に、楽しい作業が始まります。小石を落とす方法 (heapify) を使用して、ピラミッドを下から上に並べ替えましょう。最終階(2 3 9 4)から並べ替えを開始することもできますが、意味がありません。以下に転落する可能性のある床はありません。
したがって、最後から 2 番目のフロア (0 7) から要素をドロップし始めます。
⠀⠀5
⠀0⠀7
2 3 9 4
最初に該当する要素が右から選択されます。この場合は 7 です。次に、その下にあるものを調べます。その下には 9 と 4 があり、9 は 4 より大きく、9 はより大きいです。セブン! 7 を 9 に落とし、9 を持ち上げて 7 の位置に置きます。
⠀⠀5
⠀0⠀9
2 3 7 4
次に、7 には下に落ちるところがないことがわかり、左側の最後から 2 番目の階にある番号 0 に進みます。
⠀⠀5
⠀0⠀9
2 3 7 4
その下にあるものを見てみましょう – 2 と 3、2 は 3 より小さく、3 は 0 より大きいので、0 と 3 を交換します。
⠀⠀5
⠀3⠀9
2 0 7 4
フロアの端に到達したら、上のフロアに行き、可能であればそこにすべてを落としてください。
結果はデータ構造、つまりヒープ、つまり最大ヒープになります。一番上にあるのは最大の要素です。
⠀⠀9
⠀3⠀7
2 0 5 4
これを配列表現に戻すと、リストが得られます。
[9、3、7、2、0、5、4]
このことから、最初と最後の要素を交換することで、最終的な並べ替え位置の最初の数値が得られる、つまり 9 が並べ替えられたリストの最後にあるはずであると結論付けることができ、場所を入れ替えます。
[4、3、7、2、0、5、9]
二分木を見てみましょう:
⠀⠀4
⠀3⠀7
2 0 5 9
結果は、ツリーの下の部分がソートされた状況になります。必要なのは、4 を正しい位置にドロップし、アルゴリズムを繰り返すだけです。ただし、すでにソートされている数値、つまり 9 は考慮しません。
⠀⠀4
⠀3⠀7
2 0 5 9
⠀⠀7
⠀3⠀4
2 0 5 9
⠀⠀7
⠀3⠀5
2 0 4 9
4 を落とした後、9 – の次に大きな数字を上げたことが判明しました。 7. ソートされていない最後の数字 (4) と最大の数字 (7) を交換します
⠀⠀4
⠀3⠀5
2 0 7 9
正しい最終位置に 2 つの数値があることがわかりました。
4、3、5、2、0、7、9
次に、既に並べ替えられたアルゴリズムを無視して並べ替えアルゴリズムを繰り返します。最終的には ヒープ タイプ:
⠀⠀0
⠀2⠀3
4 5 7 9
またはリストとして:
0、2、3、4、5、7、9
実装
アルゴリズムは通常、次の 3 つの機能に分割されます。
<オル>
ヒープは、heapify 関数を使用してバイナリ ツリーの最後から 2 番目の行を右から左に配列の末尾まで走査することによって作成されます。次にサイクルでは、最初の数値の置換が行われ、その後、最初の要素が配置されるか、その位置に残ります。その結果、最大の要素が 1 位に配置され、参加者が 1 人減ってサイクルが繰り返されます。各パスの後、ソートされた数値がリストの最後に残ります。
Ruby でのヒープソートの例:
module Colors
BLUE = "\033[94m"
RED = "\033[31m"
STOP = "\033[0m"
end
def heapsort(rawNumbers)
numbers = rawNumbers.dup
def swap(numbers, from, to)
temp = numbers[from]
numbers[from] = numbers[to]
numbers[to] = temp
end
def heapify(numbers)
count = numbers.length()
lastParentNode = (count - 2) / 2
for start in lastParentNode.downto(0)
siftDown(numbers, start, count - 1)
start -= 1
end
if DEMO
puts "--- heapify ends ---"
end
end
def siftDown(numbers, start, rightBound)
cursor = start
printBinaryHeap(numbers, cursor, rightBound)
def calculateLhsChildIndex(cursor)
return cursor * 2 + 1
end
def calculateRhsChildIndex(cursor)
return cursor * 2 + 2
end
while calculateLhsChildIndex(cursor) <= rightBound
lhsChildIndex = calculateLhsChildIndex(cursor)
rhsChildIndex = calculateRhsChildIndex(cursor)
lhsNumber = numbers[lhsChildIndex]
biggerChildIndex = lhsChildIndex
if rhsChildIndex <= rightBound
rhsNumber = numbers[rhsChildIndex]
if lhsNumber < rhsNumber
biggerChildIndex = rhsChildIndex
end
end
if numbers[cursor] < numbers[biggerChildIndex]
swap(numbers, cursor, biggerChildIndex)
cursor = biggerChildIndex
else
break
end
printBinaryHeap(numbers, cursor, rightBound)
end
printBinaryHeap(numbers, cursor, rightBound)
end
def printBinaryHeap(numbers, nodeIndex = -1, rightBound = -1)
if DEMO == false
return
end
perLineWidth = (numbers.length() * 4).to_i
linesCount = Math.log2(numbers.length()).ceil()
xPrinterCount = 1
cursor = 0
spacing = 3
for y in (0..linesCount)
line = perLineWidth.times.map { " " }
spacing = spacing == 3 ? 4 : 3
printIndex = (perLineWidth / 2) - (spacing * xPrinterCount) / 2
for x in (0..xPrinterCount - 1)
if cursor >= numbers.length
break
end
if nodeIndex != -1 && cursor == nodeIndex
line[printIndex] = "%s%s%s" % [Colors::RED, numbers[cursor].to_s, Colors::STOP]
elsif rightBound != -1 && cursor > rightBound
line[printIndex] = "%s%s%s" % [Colors::BLUE, numbers[cursor].to_s, Colors::STOP]
else
line[printIndex] = numbers[cursor].to_s
end
cursor += 1
printIndex += spacing
end
print line.join()
xPrinterCount *= 2
print "\n"
end
end
heapify(numbers)
rightBound = numbers.length() - 1
while rightBound > 0
swap(numbers, 0, rightBound)
rightBound -= 1
siftDown(numbers, 0, rightBound)
end
return numbers
end
numbersCount = 14
maximalNumber = 10
numbers = numbersCount.times.map { Random.rand(maximalNumber) }
print numbers
print "\n---\n"
start = Time.now
sortedNumbers = heapsort(numbers)
finish = Time.now
heapSortTime = start - finish
start = Time.now
referenceSortedNumbers = numbers.sort()
finish = Time.now
referenceSortTime = start - finish
print "Reference sort: "
print referenceSortedNumbers
print "\n"
print "Reference sort time: %f\n" % referenceSortTime
print "Heap sort: "
print sortedNumbers
print "\n"
if DEMO == false
print "Heap sort time: %f\n" % heapSortTime
else
print "Disable DEMO for performance measure\n"
end
if sortedNumbers != referenceSortedNumbers
puts "Validation failed"
exit 1
else
puts "Validation success"
exit 0
end
このアルゴリズムは視覚化しないと理解しにくいため、最初にバイナリ ツリーの現在のビューを出力する関数を作成することをお勧めします。
リンク
https://gitlab.com/demensdeum/algorithms/-/blob/master/sortAlgorithms/heapsort/heapsort.rb
ソース
http://rosettacode.org/wiki/Sorting_algorithms/Heapsort
https://www.youtube.com/watch?v=LbB357_RwlY
https://habr.com/ru/company/ otus/blog/460087/
https://ru.wikipedia.org/wiki/Pyramid_sort
https://neerc.ifmo.ru/wiki /index.php?title=ヒープソート
https://wiki5.ru/wiki/Heapsort
https://ru.wikipedia.org/wiki/Tree (データ構造)
https://ru.wikipedia.org/wiki/Heap (データ構造)
https://www.youtube.com/watch?v=2DmK_H7IdTo
https://www.youtube.com/watch?v=kU4KBD4NFtw
https://www.youtube.com/watch?v=DU1uG5310x0
https://www.youtube.com/watch?v =BzQGPA_v-vc
https://www.geeksforgeeks.org/バイナリヒープの配列表現/
https://habr.com/ru/post/112222/
https://www.cs.usfca. edu/~galles/visualization/BST.html
https://www.youtube.com/watch?v=EQzqHWtsKq4
https://ru.wikibrief.org/wiki/Heapsort
https://www.youtube.com/watch?v=GUUpmrTnNbw
クイックソート
クイックソートは分割統治型の並べ替えアルゴリズムです。再帰的に、部分ごとに数値の配列を解析し、選択した参照要素から小さい順に大きい順に数値を配置し、参照要素自体をそれらの間のカットオフに挿入します。何度か再帰的に繰り返すと、ソートされたリストが完成します。時間計算量 O(n2)。
スキーム:
<オル>
クイックソートは、モスクワ州立大学の科学者チャールズ アンソニー リチャード ホアによって発明されました。彼はロシア語を学び、コルモゴロフ学校でコンピューター翻訳と確率論を学びました。 1960 年、政治危機のため、彼はソ連を去りました。
Rust での実装例:
use rand::Rng;
fn swap(numbers: &mut [i64], from: usize, to: usize) {
let temp = numbers[from];
numbers[from] = numbers[to];
numbers[to] = temp;
}
fn quicksort(numbers: &mut [i64], left: usize, right: usize) {
if left >= right {
return
}
let length = right - left;
if length <= 1 {
return
}
let pivot_index = left + (length / 2);
let pivot = numbers[pivot_index];
let last_index = right - 1;
swap(numbers, pivot_index, last_index);
let mut less_insert_index = left;
for i in left..last_index {
if numbers[i] < pivot {
swap(numbers, i, less_insert_index);
less_insert_index += 1;
}
}
swap(numbers, last_index, less_insert_index);
quicksort(numbers, left, less_insert_index);
quicksort(numbers, less_insert_index + 1, right);
}
fn main() {
let mut numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut reference_numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut rng = rand::thread_rng();
for i in 0..numbers.len() {
numbers[i] = rng.gen_range(-10..10);
reference_numbers[i] = numbers[i];
}
reference_numbers.sort();
println!("Numbers {:?}", numbers);
let length = numbers.len();
quicksort(&mut numbers, 0, length);
println!("Numbers {:?}", numbers);
println!("Reference numbers {:?}", reference_numbers);
if numbers != reference_numbers {
println!("Validation failed");
std::process::exit(1);
}
else {
println!("Validation success!");
std::process::exit(0);
}
}
何も明確でない場合は、サンディエゴ大学の Rob Edwards によるビデオを見ることをお勧めします https://www.youtube.com/watch?v=ZHVk2blR45Q アルゴリズムの本質と実装をステップごとに最も簡単に示しています。
リンク
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/quickSort
ソース
https://www.youtube.com/watch?v =4s-aG6yGGLU
https://www.youtube.com/watch?v=ywWBy6J5gz8
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://ru.wikipedia.org/wiki/Быстрая_сортировка
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://www.youtube.com/watch?v=XE4VP_8Y0BU
https://www.youtube.com/watch?v=MZaf_9IZCrc
https://www.youtube.com/watch?v=ZHVk2blR45Q
http://rosettacode.org/wiki/Sorting_algorithms/Quicksort
https://www.youtube.com/watch?v=4s-aG6yGGLU
https://www.youtube.com/watch?v=dQw4w9WgXcQ
https://www.youtube.com/watch?v=maibrCbZWKw
https://www.geeksforgeeks.org/quick-sort/
https://www.youtube.com/watch?v=uXBnyYuwPe8
バイナリ挿入ソート
二分挿入ソートは、二分検索を使用して挿入位置を決定する挿入ソートの変形です。アルゴリズムの時間計算量は O(n2) です
アルゴリズムは次のように機能します:
<オル>
バイナリ検索中に、数値が見つからず、インデックスが返されない可能性があります。二分検索の特殊性により、検索された数値に最も近い数値が検索され、インデックスを返すには、そのインデックスを求めた数値と比較する必要があります。求めた数値が小さい場合、求めた数値は次の位置にある必要があります。インデックスが左側にあり、それ以上の場合は右側にあります。
Go コード:
import (
"fmt"
"math/rand"
"time"
)
const numbersCount = 20
const maximalNumber = 100
func binarySearch(numbers []int, item int, low int, high int) int {
for high > low {
center := (low + high) / 2
if numbers[center] < item { low = center + 1 } else if numbers[center] > item {
high = center - 1
} else {
return center
}
}
if numbers[low] < item {
return low + 1
} else {
return low
}
}
func main() {
rand.Seed(time.Now().Unix())
var numbers [numbersCount]int
for i := 0; i < numbersCount; i++ {
numbers[i] = rand.Intn(maximalNumber)
}
fmt.Println(numbers)
for i := 1; i < len(numbers); i++ { searchAreaLastIndex := i - 1 insertNumber := numbers[i] insertIndex := binarySearch(numbers[:], insertNumber, 0, searchAreaLastIndex) for x := searchAreaLastIndex; x >= insertIndex; x-- {
numbers[x+1] = numbers[x]
}
numbers[insertIndex] = insertNumber
}
fmt.Println(numbers)
}
リンク
ソース
https://www.geeksforgeeks.org/binary-insertion-並べ替え/
https://www.youtube.com/watch?v=-OVB5pOZJug
シェルソート
シェル ソート – 数値の配列を事前に組み合わせた挿入ソートの変形です。
挿入ソートがどのように機能するかを覚えておく必要があります。
1.ループは0からループの終わりまで開始されるため、配列は2つの部分に分割されます
2. 左側の部分では、2 番目のループが開始され、要素を右から左に比較します。左側の小さい要素が見つかるまで、右側の小さい要素が削除されます。
3. 両方のループの最後に、ソートされたリストが得られます。
昔々、コンピューター科学者のドナルド シェルは、挿入ソート アルゴリズムを改善する方法を考えていました。彼はまた、最初に配列を 2 サイクルで処理するが、一定の距離を置き、通常の挿入ソート アルゴリズムに変わるまで「コーム」を徐々に減らしていくというアイデアも思いつきました。すべては非常に単純で、落とし穴はありません。上記の 2 つのサイクルに別のサイクルを追加し、「コーム」のサイズを徐々に小さくします。必要なのは、比較するときに配列を超えないよう距離を確認することだけです。
本当に興味深いトピックは、最初のループの各反復で比較長を変更するためのシーケンスを選択することです。アルゴリズムのパフォーマンスがアルゴリズムに依存するという理由から、これは興味深いものです。
既知のオプションと時間計算量の表は、https: //en .wikipedia.org/wiki/Shellsort#Gap_sequences
理想的な距離の計算にはさまざまな人々が関与しており、このトピックは彼らにとって非常に興味深いものだったようです。 Ruby を実行して、最速の sort() アルゴリズムを呼び出すことはできないでしょうか?
一般に、これらの奇妙な人々は、シェル アルゴリズムの「櫛」の距離/ギャップの計算をテーマに論文を書きました。私は彼らの研究結果を単純に使用し、Hibbard、Knuth-Pratt、Chiura、Sedgwick の 5 種類のシーケンスをチェックしました。
import time
import random
from functools import reduce
import math
DEMO_MODE = False
if input("Demo Mode Y/N? ").upper() == "Y":
DEMO_MODE = True
class Colors:
BLUE = '\033[94m'
RED = '\033[31m'
END = '\033[0m'
def swap(list, lhs, rhs):
list[lhs], list[rhs] = list[rhs], list[lhs]
return list
def colorPrintoutStep(numbers: List[int], lhs: int, rhs: int):
for index, number in enumerate(numbers):
if index == lhs:
print(f"{Colors.BLUE}", end = "")
elif index == rhs:
print(f"{Colors.RED}", end = "")
print(f"{number},", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
print("\n")
input(">")
def ShellSortLoop(numbers: List[int], distanceSequence: List[int]):
distanceSequenceIterator = reversed(distanceSequence)
while distance:= next(distanceSequenceIterator, None):
for sortArea in range(0, len(numbers)):
for rhs in reversed(range(distance, sortArea + 1)):
lhs = rhs - distance
if DEMO_MODE:
print(f"Distance: {distance}")
colorPrintoutStep(numbers, lhs, rhs)
if numbers[lhs] > numbers[rhs]:
swap(numbers, lhs, rhs)
else:
break
def ShellSort(numbers: List[int]):
global ShellSequence
ShellSortLoop(numbers, ShellSequence)
def HibbardSort(numbers: List[int]):
global HibbardSequence
ShellSortLoop(numbers, HibbardSequence)
def ShellPlusKnuttPrattSort(numbers: List[int]):
global KnuttPrattSequence
ShellSortLoop(numbers, KnuttPrattSequence)
def ShellPlusCiuraSort(numbers: List[int]):
global CiuraSequence
ShellSortLoop(numbers, CiuraSequence)
def ShellPlusSedgewickSort(numbers: List[int]):
global SedgewickSequence
ShellSortLoop(numbers, SedgewickSequence)
def insertionSort(numbers: List[int]):
global insertionSortDistanceSequence
ShellSortLoop(numbers, insertionSortDistanceSequence)
def defaultSort(numbers: List[int]):
numbers.sort()
def measureExecution(inputNumbers: List[int], algorithmName: str, algorithm):
if DEMO_MODE:
print(f"{algorithmName} started")
numbers = inputNumbers.copy()
startTime = time.perf_counter()
algorithm(numbers)
endTime = time.perf_counter()
print(f"{algorithmName} performance: {endTime - startTime}")
def sortedNumbersAsString(inputNumbers: List[int], algorithm) -> str:
numbers = inputNumbers.copy()
algorithm(numbers)
return str(numbers)
if DEMO_MODE:
maximalNumber = 10
numbersCount = 10
else:
maximalNumber = 10
numbersCount = random.randint(10000, 20000)
randomNumbers = [random.randrange(1, maximalNumber) for i in range(numbersCount)]
ShellSequenceGenerator = lambda n: reduce(lambda x, _: x + [int(x[-1]/2)], range(int(math.log(numbersCount, 2))), [int(numbersCount / 2)])
ShellSequence = ShellSequenceGenerator(randomNumbers)
ShellSequence.reverse()
ShellSequence.pop()
HibbardSequence = [
0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095,
8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575,
2097151, 4194303, 8388607, 16777215, 33554431, 67108863, 134217727,
268435455, 536870911, 1073741823, 2147483647, 4294967295, 8589934591
]
KnuttPrattSequence = [
1, 4, 13, 40, 121, 364, 1093, 3280, 9841, 29524, 88573, 265720,
797161, 2391484, 7174453, 21523360, 64570081, 193710244, 581130733,
1743392200, 5230176601, 15690529804, 47071589413
]
CiuraSequence = [
1, 4, 10, 23, 57, 132, 301, 701, 1750, 4376,
10941, 27353, 68383, 170958, 427396, 1068491,
2671228, 6678071, 16695178, 41737946, 104344866,
260862166, 652155416, 1630388541
]
SedgewickSequence = [
1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905,
8929, 16001, 36289, 64769, 146305, 260609, 587521,
1045505, 2354689, 4188161, 9427969, 16764929, 37730305,
67084289, 150958081, 268386305, 603906049, 1073643521,
2415771649, 4294770689, 9663381505, 17179475969
]
insertionSortDistanceSequence = [1]
algorithms = {
"Default Python Sort": defaultSort,
"Shell Sort": ShellSort,
"Shell + Hibbard" : HibbardSort,
"Shell + Prat, Knutt": ShellPlusKnuttPrattSort,
"Shell + Ciura Sort": ShellPlusCiuraSort,
"Shell + Sedgewick Sort": ShellPlusSedgewickSort,
"Insertion Sort": insertionSort
}
for name, algorithm in algorithms.items():
measureExecution(randomNumbers, name, algorithm)
reference = sortedNumbersAsString(randomNumbers, defaultSort)
for name, algorithm in algorithms.items():
if sortedNumbersAsString(randomNumbers, algorithm) != reference:
print("Sorting validation failed")
exit(1)
print("Sorting validation success")
exit(0)
私の実装では、ランダムな数値セットの場合、最も速いギャップはセジウィックとヒバードです。
マイピー
Python 3 – の静的型付けアナライザーについても触れておきたいと思います。マイピー。動的型付けを使用する言語に固有の問題に対処するのに役立ちます。つまり、不必要な場所に何かが貼り付けられる可能性を排除します。
経験豊富なプログラマーが言うように、「専門家のチームがいる場合、静的型付けは必要ありません」。いつか私たち全員が専門家になり、完全に統一してマシンを理解しながらコードを書くようになりますが、今のところは同様のユーティリティを使用できます。静的型付け言語。
リンク
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/shellSort
http://mypy-lang.org/
ソース
https://dl.acm.org/doi/10.1145/368370.368387
https://en.wikipedia.org/wiki/Shellsort
http://rosettacode.org/wiki/Sorting_algorithms/Shell_sort
https://ru.wikipedia.org/wiki/Сортировка_Шелла
https://neerc.ifmo.ru/wiki/index.php?title=Сортировка_Шелла
https://twitter.com/gvanrossum/status/700741601966985216
二重選択ソート
Double Selection Sort – 選択ソートのサブタイプで、速度が 2 倍になるようです。バニラのアルゴリズムは、数値のリストを 2 回ループし、最小の数値を見つけて、上のレベルのループが指す現在の数値と位置を交換します。二重選択ソートでは、最小値と最大値を検索し、– より上のレベルでループが指す 2 桁を置き換えます。左右に 2 つの数字。この乱交全体は、置換される数字のカーソルがリストの中央に見つかると終了します。その結果、ソートされた数字が視覚的中心の左右に取得されます。
アルゴリズムの時間計算量は、選択ソートと同様です。 O(n2) ですが、おそらく 30 の加速度があると思われます%。
境界線の状態
この段階ですでに、衝突の瞬間を想像することができます。たとえば、左カーソルの番号 (最小値) がリスト内の最大値を指しているとき、最小値が再配置され、再配置が行われます。最大数がすぐに壊れてしまいます。したがって、アルゴリズムのすべての実装には、そのようなケースのチェックとインデックスの正しいものへの置き換えが含まれます。私の実装では、1 回のチェックで十分でした。
maximalNumberIndex = minimalNumberIndex;
}Реализация на Cito
Cito – язык либ, язык транслятор. На нем можно писать для C, C++, C#, Java, JavaScript, Python, Swift, TypeScript, OpenCL C, при этом совершенно ничего не зная про эти языки. Исходный код на языке Cito транслируется в исходный код на поддерживаемых языках, далее можно использовать как библиотеку, либо напрямую, исправив сгенеренный код руками. Эдакий Write once – translate to anything.
Double Selection Sort на cito:
{
public static int[] sort(int[]# numbers, int length)
{
int[]# sortedNumbers = new int[length];
for (int i = 0; i < length; i++) {
sortedNumbers[i] = numbers[i];
}
for (int leftCursor = 0; leftCursor < length / 2; leftCursor++) {
int minimalNumberIndex = leftCursor;
int minimalNumber = sortedNumbers[leftCursor];
int rightCursor = length - (leftCursor + 1);
int maximalNumberIndex = rightCursor;
int maximalNumber = sortedNumbers[maximalNumberIndex];
for (int cursor = leftCursor; cursor <= rightCursor; cursor++) { int cursorNumber = sortedNumbers[cursor]; if (minimalNumber > cursorNumber) {
minimalNumber = cursorNumber;
minimalNumberIndex = cursor;
}
if (maximalNumber < cursorNumber) {
maximalNumber = cursorNumber;
maximalNumberIndex = cursor;
}
}
if (leftCursor == maximalNumberIndex) {
maximalNumberIndex = minimalNumberIndex;
}
int fromNumber = sortedNumbers[leftCursor];
int toNumber = sortedNumbers[minimalNumberIndex];
sortedNumbers[minimalNumberIndex] = fromNumber;
sortedNumbers[leftCursor] = toNumber;
fromNumber = sortedNumbers[rightCursor];
toNumber = sortedNumbers[maximalNumberIndex];
sortedNumbers[maximalNumberIndex] = fromNumber;
sortedNumbers[rightCursor] = toNumber;
}
return sortedNumbers;
}
}
リンク
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/doubleSelectionSort
https://github.com/pfusik/cito
ソース
https://www.researchgate.net/publication/330084245_改良_Double_Selection_Sort_using_Algorithm
http://algolab.valemak.com/selection-double
https://www.geeksforgeeks.org/sorting-algorithm-slightly-improves-selection-sort/