tree sort

树排序——使用二叉搜索树进行排序。时间复杂度– O(n²)。在这样的树中，左边的每个节点都有小于该节点的数字，右边的每个节点都有大于该节点的数字，当从根开始并从左到右打印值时，我们得到一个排序的数字列表。令人惊讶吧？

考虑二叉搜索树图：

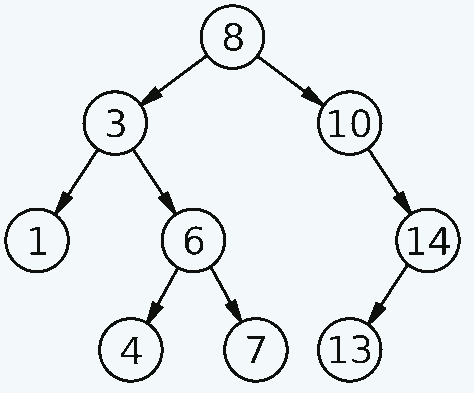
Derrick Coetzee（公共领域）

尝试手动读取从左下角倒数第二个左侧节点开始的数字，对于左侧的每个节点 – 右侧的一个节点。

它看起来像这样：

左下角倒数第二个节点 – 3.
它有一个左分支 – 1.
取这个数字（1）
接下来我们采用顶点 3 (1, 3)
右侧是分支 6，但它包含分支。因此，我们以同样的方式阅读它。
节点 6 编号 4 的左分支 (1, 3, 4)
节点本身为 6 (1, 3, 4, 6)
右 7（1、3、4、6、7）
向上到根节点– 8（1,3,4,6,7,8）
我们以此类推将所有内容打印在右侧
我们得到了最终名单– 1、3、4、6、7、8、10、13、14

要在代码中实现该算法，您需要两个函数：

组装二叉搜索树
以正确的顺序打印二叉搜索树

二叉搜索树的组装方式与读取时相同，左侧或右侧的每个节点都会附加一个数字，具体取决于它是较少还是较多。

Lua 中的示例：


function Node:new(value, lhs, rhs)
    output = {}
    setmetatable(output, self)
    self.__index = self  
    output.value = value
    output.lhs = lhs
    output.rhs = rhs
    output.counter = 1
    return output  
end

function Node:Increment()
    self.counter = self.counter + 1
end

function Node:Insert(value)
    if self.lhs ~= nil and self.lhs.value > value then
        self.lhs:Insert(value)
        return
    end

    if self.rhs ~= nil and self.rhs.value < value then
        self.rhs:Insert(value)
        return
    end

    if self.value == value then
        self:Increment()
        return
    elseif self.value > value then
        if self.lhs == nil then
            self.lhs = Node:new(value, nil, nil)
        else
            self.lhs:Insert(value)
        end
        return
    else
        if self.rhs == nil then
            self.rhs = Node:new(value, nil, nil)
        else
            self.rhs:Insert(value)
        end
        return
    end
end

function Node:InOrder(output)
    if self.lhs ~= nil then
       output = self.lhs:InOrder(output)
    end
    output = self:printSelf(output)
    if self.rhs ~= nil then
        output = self.rhs:InOrder(output)
    end
    return output
end

function Node:printSelf(output)
    for i=0,self.counter-1 do
        output = output .. tostring(self.value) .. " "
    end
    return output
end

function PrintArray(numbers)
    output = ""
    for i=0,#numbers do
        output = output .. tostring(numbers[i]) .. " "
    end    
    print(output)
end

function Treesort(numbers)
    rootNode = Node:new(numbers[0], nil, nil)
    for i=1,#numbers do
        rootNode:Insert(numbers[i])
    end
    print(rootNode:InOrder(""))
end


numbersCount = 10
maxNumber = 9

numbers = {}

for i=0,numbersCount-1 do
    numbers[i] = math.random(0, maxNumber)
end

PrintArray(numbers)
Treesort(numbers)

Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.