tree sort

Baumsortierung – Sortierung mithilfe eines binären Suchbaums. Zeitkomplexität – O(n²). In einem solchen Baum hat jeder Knoten links Zahlen, die kleiner sind als der Knoten, rechts sind es mehr als der Knoten. Wenn wir von der Wurzel kommen und die Werte von links nach rechts drucken, erhalten wir eine sortierte Liste von Zahlen . Überraschend, oder?

Betrachten Sie das binäre Suchbaumdiagramm:

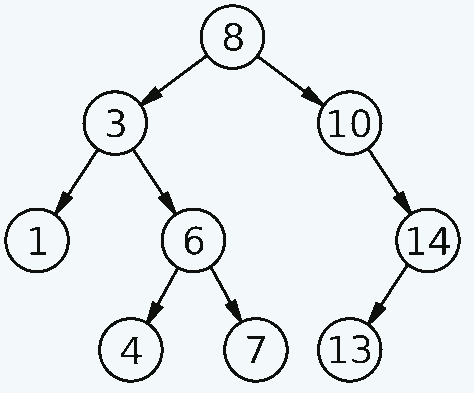
Derrick Coetzee (gemeinfrei)

Versuchen Sie, die Zahlen manuell abzulesen, beginnend beim vorletzten linken Knoten der unteren linken Ecke, für jeden Knoten links – einen Knoten – rechts.

Es wird so aussehen:

Vorletzter Knoten unten links – 3.
Es hat einen linken Zweig – 1.
Nehmen Sie diese Nummer (1)
Als nächstes nehmen wir Scheitelpunkt 3 (1, 3)
Auf der rechten Seite befindet sich Zweig 6, der jedoch Zweige enthält. Deshalb lesen wir es genauso.
Linker Zweig von Knoten 6 Nummer 4 (1, 3, 4)
Der Knoten selbst ist 6 (1, 3, 4, 6)
Rechts 7 (1, 3, 4, 6, 7)
Gehen Sie zum Wurzelknoten hoch – 8 (1,3, 4,6, 7, 8)
Alles auf der rechten Seite drucken wir analog aus
Wir erhalten die endgültige Liste – 1, 3, 4, 6, 7, 8, 10, 13, 14

Um den Algorithmus im Code zu implementieren, benötigen Sie zwei Funktionen:

Zusammenstellen eines binären Suchbaums
Den binären Suchbaum in der richtigen Reihenfolge ausdrucken

Der binäre Suchbaum wird auf die gleiche Weise zusammengestellt, wie er gelesen wird. An jeden Knoten wird links oder rechts eine Zahl angehängt, je nachdem, ob er kleiner oder größer ist.

Beispiel in Lua:


function Node:new(value, lhs, rhs)
    output = {}
    setmetatable(output, self)
    self.__index = self  
    output.value = value
    output.lhs = lhs
    output.rhs = rhs
    output.counter = 1
    return output  
end

function Node:Increment()
    self.counter = self.counter + 1
end

function Node:Insert(value)
    if self.lhs ~= nil and self.lhs.value > value then
        self.lhs:Insert(value)
        return
    end

    if self.rhs ~= nil and self.rhs.value < value then
        self.rhs:Insert(value)
        return
    end

    if self.value == value then
        self:Increment()
        return
    elseif self.value > value then
        if self.lhs == nil then
            self.lhs = Node:new(value, nil, nil)
        else
            self.lhs:Insert(value)
        end
        return
    else
        if self.rhs == nil then
            self.rhs = Node:new(value, nil, nil)
        else
            self.rhs:Insert(value)
        end
        return
    end
end

function Node:InOrder(output)
    if self.lhs ~= nil then
       output = self.lhs:InOrder(output)
    end
    output = self:printSelf(output)
    if self.rhs ~= nil then
        output = self.rhs:InOrder(output)
    end
    return output
end

function Node:printSelf(output)
    for i=0,self.counter-1 do
        output = output .. tostring(self.value) .. " "
    end
    return output
end

function PrintArray(numbers)
    output = ""
    for i=0,#numbers do
        output = output .. tostring(numbers[i]) .. " "
    end    
    print(output)
end

function Treesort(numbers)
    rootNode = Node:new(numbers[0], nil, nil)
    for i=1,#numbers do
        rootNode:Insert(numbers[i])
    end
    print(rootNode:InOrder(""))
end


numbersCount = 10
maxNumber = 9

numbers = {}

for i=0,numbersCount-1 do
    numbers[i] = math.random(0, maxNumber)
end

PrintArray(numbers)
Treesort(numbers)

Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.