tree sort

Tri par arbre : tri à l’aide d’un arbre de recherche binaire. Complexité temporelle – O(n²). Dans un tel arbre, chaque nœud à gauche a des nombres inférieurs au nœud, à droite il y en a plus que le nœud, en venant de la racine et en imprimant les valeurs de gauche à droite, on obtient une liste triée de nombres . Surprenant, non ?

Considérez l’arbre de recherche binaire :

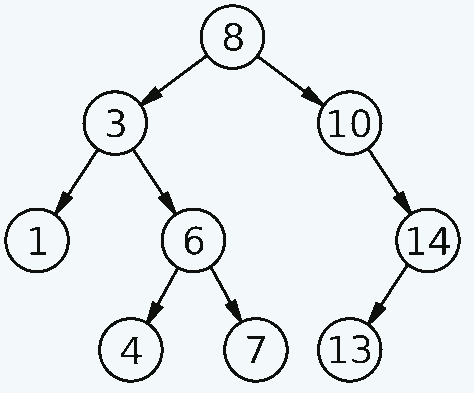
Derrick Coetzee (domaine public)

Essayez de lire manuellement les nombres en partant de l’avant-dernier nœud gauche du coin inférieur gauche, pour chaque nœud à gauche – un nœud – à droite.

Cela ressemblera à ceci :

Avant-dernier nœud en bas à gauche – 3.
Il a une branche gauche – 1.
Prenez ce numéro (1)
Ensuite, nous prenons le sommet 3 (1, 3)
À droite se trouve la branche 6, mais elle contient des branches. Par conséquent, nous le lisons de la même manière.
Branche gauche du nœud 6 numéro 4 (1, 3, 4)
Le nœud lui-même est 6 (1, 3, 4, 6)
Droite 7 (1, 3, 4, 6, 7)
Montez jusqu’au nœud racine – 8 (1,3, 4,6, 7, 8)
Nous imprimons tout à droite par analogie
Nous obtenons la liste finale – 1, 3, 4, 6, 7, 8, 10, 13, 14

Pour implémenter l’algorithme dans le code, vous aurez besoin de deux fonctions :

Assembler un arbre de recherche binaire
Imprimer l’arbre de recherche binaire dans le bon ordre

L’arbre binaire de recherche est assemblé de la même manière qu’il est lu, un numéro est attaché à chaque nœud à gauche ou à droite, selon qu’il est inférieur ou supérieur.

Exemple en Lua :


function Node:new(value, lhs, rhs)
    output = {}
    setmetatable(output, self)
    self.__index = self  
    output.value = value
    output.lhs = lhs
    output.rhs = rhs
    output.counter = 1
    return output  
end

function Node:Increment()
    self.counter = self.counter + 1
end

function Node:Insert(value)
    if self.lhs ~= nil and self.lhs.value > value then
        self.lhs:Insert(value)
        return
    end

    if self.rhs ~= nil and self.rhs.value < value then
        self.rhs:Insert(value)
        return
    end

    if self.value == value then
        self:Increment()
        return
    elseif self.value > value then
        if self.lhs == nil then
            self.lhs = Node:new(value, nil, nil)
        else
            self.lhs:Insert(value)
        end
        return
    else
        if self.rhs == nil then
            self.rhs = Node:new(value, nil, nil)
        else
            self.rhs:Insert(value)
        end
        return
    end
end

function Node:InOrder(output)
    if self.lhs ~= nil then
       output = self.lhs:InOrder(output)
    end
    output = self:printSelf(output)
    if self.rhs ~= nil then
        output = self.rhs:InOrder(output)
    end
    return output
end

function Node:printSelf(output)
    for i=0,self.counter-1 do
        output = output .. tostring(self.value) .. " "
    end
    return output
end

function PrintArray(numbers)
    output = ""
    for i=0,#numbers do
        output = output .. tostring(numbers[i]) .. " "
    end    
    print(output)
end

function Treesort(numbers)
    rootNode = Node:new(numbers[0], nil, nil)
    for i=1,#numbers do
        rootNode:Insert(numbers[i])
    end
    print(rootNode:InOrder(""))
end


numbersCount = 10
maxNumber = 9

numbers = {}

for i=0,numbersCount-1 do
    numbers[i] = math.random(0, maxNumber)
end

PrintArray(numbers)
Treesort(numbers)

Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.