tree sort

Classificação em árvore – classificação usando uma árvore de pesquisa binária. Complexidade de tempo – O(n²). Nessa árvore, cada nó da esquerda tem números menores que o nó, à direita há mais que o nó, ao vir da raiz e imprimir os valores da esquerda para a direita, obtemos uma lista ordenada de números . Surpreendente, certo?

Considere o diagrama de árvore de pesquisa binária:

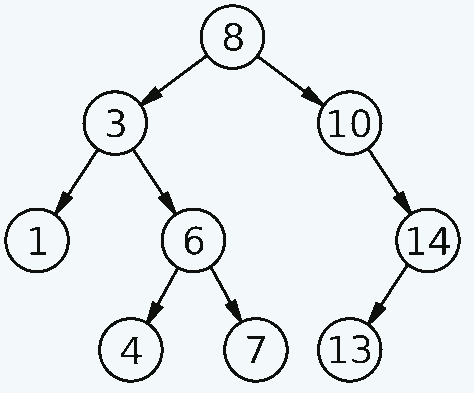
Derrick Coetzee (domínio público)

Tente ler manualmente os números começando pelo penúltimo nó esquerdo do canto inferior esquerdo, para cada nó à esquerda – um nó – à direita.

Ficará assim:

Penúltimo nó no canto inferior esquerdo – 3.
Tem um ramo esquerdo – 1.
Pegue este número (1)
Em seguida, pegamos o vértice 3 (1, 3)
À direita está o ramo 6, mas contém ramos. Portanto, lemos da mesma maneira.
Ramo esquerdo do nó 6 número 4 (1, 3, 4)
O próprio nó é 6 (1, 3, 4, 6)
Direita 7 (1, 3, 4, 6, 7)
Vá até o nó raiz – 8 (1,3, 4,6, 7, 8)
Imprimimos tudo à direita por analogia
Obtemos a lista final – 1, 3, 4, 6, 7, 8, 10, 13, 14

Para implementar o algoritmo em código, você precisará de duas funções:

Montando uma árvore de pesquisa binária
Imprimindo a árvore de pesquisa binária na ordem correta

A árvore binária de busca é montada da mesma forma que é lida, um número é anexado a cada nó à esquerda ou à direita, dependendo se é menor ou maior.

Exemplo em Lua:


function Node:new(value, lhs, rhs)
    output = {}
    setmetatable(output, self)
    self.__index = self  
    output.value = value
    output.lhs = lhs
    output.rhs = rhs
    output.counter = 1
    return output  
end

function Node:Increment()
    self.counter = self.counter + 1
end

function Node:Insert(value)
    if self.lhs ~= nil and self.lhs.value > value then
        self.lhs:Insert(value)
        return
    end

    if self.rhs ~= nil and self.rhs.value < value then
        self.rhs:Insert(value)
        return
    end

    if self.value == value then
        self:Increment()
        return
    elseif self.value > value then
        if self.lhs == nil then
            self.lhs = Node:new(value, nil, nil)
        else
            self.lhs:Insert(value)
        end
        return
    else
        if self.rhs == nil then
            self.rhs = Node:new(value, nil, nil)
        else
            self.rhs:Insert(value)
        end
        return
    end
end

function Node:InOrder(output)
    if self.lhs ~= nil then
       output = self.lhs:InOrder(output)
    end
    output = self:printSelf(output)
    if self.rhs ~= nil then
        output = self.rhs:InOrder(output)
    end
    return output
end

function Node:printSelf(output)
    for i=0,self.counter-1 do
        output = output .. tostring(self.value) .. " "
    end
    return output
end

function PrintArray(numbers)
    output = ""
    for i=0,#numbers do
        output = output .. tostring(numbers[i]) .. " "
    end    
    print(output)
end

function Treesort(numbers)
    rootNode = Node:new(numbers[0], nil, nil)
    for i=1,#numbers do
        rootNode:Insert(numbers[i])
    end
    print(rootNode:InOrder(""))
end


numbersCount = 10
maxNumber = 9

numbers = {}

for i=0,numbersCount-1 do
    numbers[i] = math.random(0, maxNumber)
end

PrintArray(numbers)
Treesort(numbers)

Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.