Classificação em árvore – classificação usando uma árvore de pesquisa binária. Complexidade de tempo – O(n²). Nessa árvore, cada nó da esquerda tem números menores que o nó, à direita há mais que o nó, ao vir da raiz e imprimir os valores da esquerda para a direita, obtemos uma lista ordenada de números . Surpreendente, certo?
Considere o diagrama de árvore de pesquisa binária:
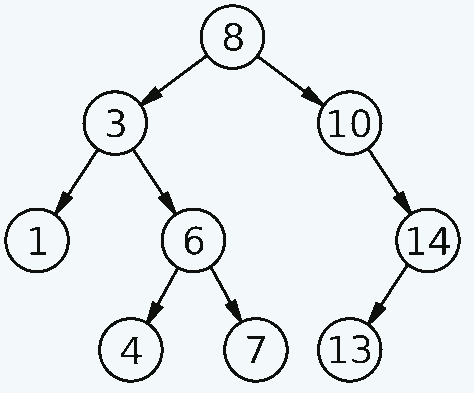
Derrick Coetzee (domínio público)
Tente ler manualmente os números começando pelo penúltimo nó esquerdo do canto inferior esquerdo, para cada nó à esquerda – um nó – à direita.
Ficará assim:
- Penúltimo nó no canto inferior esquerdo – 3.
- Tem um ramo esquerdo – 1.
- Pegue este número (1)
- Em seguida, pegamos o vértice 3 (1, 3)
- À direita está o ramo 6, mas contém ramos. Portanto, lemos da mesma maneira.
- Ramo esquerdo do nó 6 número 4 (1, 3, 4)
- O próprio nó é 6 (1, 3, 4, 6)
- Direita 7 (1, 3, 4, 6, 7)
- Vá até o nó raiz – 8 (1,3, 4,6, 7, 8)
- Imprimimos tudo à direita por analogia
- Obtemos a lista final – 1, 3, 4, 6, 7, 8, 10, 13, 14
Para implementar o algoritmo em código, você precisará de duas funções:
- Montando uma árvore de pesquisa binária
- Imprimindo a árvore de pesquisa binária na ordem correta
A árvore binária de busca é montada da mesma forma que é lida, um número é anexado a cada nó à esquerda ou à direita, dependendo se é menor ou maior.
Exemplo em Lua:
function Node:new(value, lhs, rhs)
output = {}
setmetatable(output, self)
self.__index = self
output.value = value
output.lhs = lhs
output.rhs = rhs
output.counter = 1
return output
end
function Node:Increment()
self.counter = self.counter + 1
end
function Node:Insert(value)
if self.lhs ~= nil and self.lhs.value > value then
self.lhs:Insert(value)
return
end
if self.rhs ~= nil and self.rhs.value < value then
self.rhs:Insert(value)
return
end
if self.value == value then
self:Increment()
return
elseif self.value > value then
if self.lhs == nil then
self.lhs = Node:new(value, nil, nil)
else
self.lhs:Insert(value)
end
return
else
if self.rhs == nil then
self.rhs = Node:new(value, nil, nil)
else
self.rhs:Insert(value)
end
return
end
end
function Node:InOrder(output)
if self.lhs ~= nil then
output = self.lhs:InOrder(output)
end
output = self:printSelf(output)
if self.rhs ~= nil then
output = self.rhs:InOrder(output)
end
return output
end
function Node:printSelf(output)
for i=0,self.counter-1 do
output = output .. tostring(self.value) .. " "
end
return output
end
function PrintArray(numbers)
output = ""
for i=0,#numbers do
output = output .. tostring(numbers[i]) .. " "
end
print(output)
end
function Treesort(numbers)
rootNode = Node:new(numbers[0], nil, nil)
for i=1,#numbers do
rootNode:Insert(numbers[i])
end
print(rootNode:InOrder(""))
end
numbersCount = 10
maxNumber = 9
numbers = {}
for i=0,numbersCount-1 do
numbers[i] = math.random(0, maxNumber)
end
PrintArray(numbers)
Treesort(numbers)Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/treesort
Источники
Convert Sorted Array to Binary Search Tree (LeetCode 108. Algorithm Explained) – YouTube
Sorting algorithms/Tree sort on a linked list – Rosetta Code
How to handle duplicates in Binary Search Tree? – GeeksforGeeks
Tree Sort | GeeksforGeeks – YouTube
Classificação de intervalo
Classificação por bucket – classificação por buckets. O algoritmo é semelhante à classificação por contagem, com a diferença de que os números são coletados em intervalos de “baldes”, então os baldes são classificados usando qualquer outro algoritmo de classificação suficientemente produtivo, e a etapa final é desdobrar os “baldes” um por um, resultando em uma lista ordenada
.
A complexidade de tempo do algoritmo é O(nk). O algoritmo funciona em tempo linear para dados que obedecem a uma lei de distribuição uniforme. Simplificando, os elementos devem estar em um determinado intervalo, sem “picos”, por exemplo, números de 0,0 a 1,0. Se entre esses números houver 4 ou 999, então, de acordo com as leis do pátio, essa linha não será mais considerada “par”.
Exemplo de implementação em Julia:
buckets = Vector{Vector{Int}}()
for i in 0:bucketsCount - 1
bucket = Vector{Int}()
push!(buckets, bucket)
end
maxNumber = maximum(numbers)
for i in 0:length(numbers) - 1
bucketIndex = 1 + Int(floor(bucketsCount * numbers[1 + i] / (maxNumber + 1)))
push!(buckets[bucketIndex], numbers[1 + i])
end
for i in 0:length(buckets) - 1
bucketIndex = 1 + i
buckets[bucketIndex] = sort(buckets[bucketIndex])
end
flat = [(buckets...)...]
print(flat, "\n")
end
numbersCount = 10
maxNumber = 10
numbers = rand(1:maxNumber, numbersCount)
print(numbers,"\n")
bucketsCount = 10
bucketSort(numbers, bucketsCount)На производительность алгоритма также влияет число ведер, для большего количества чисел лучше взять большее число ведер (Algorithms in a nutshell by George T. Heineman)
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/bucketSort
Источники
https://www.youtube.com/watch?v=VuXbEb5ywrU
https://www.youtube.com/watch?v=ELrhrrCjDOA
https://medium.com/karuna-sehgal/an-introduction-to-bucket-sort-62aa5325d124
https://www.geeksforgeeks.org/bucket-sort-2/
https://ru.wikipedia.org/wiki/%D0%91%D0%BB%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0
https://www.youtube.com/watch?v=LPrF9yEKTks
https://en.wikipedia.org/wiki/Bucket_sort
https://julialang.org/
https://www.oreilly.com/library/view/algorithms-in-a/9780596516246/ch04s08.html
Radixsort
Classificação de raiz – classificação de raiz. O algoritmo é semelhante à classificação por contagem, pois não há comparação de elementos; em vez disso, os elementos são agrupados *caractere por caractere* em *baldes* (baldes), o balde é selecionado pelo índice do caractere numérico atual. Complexidade de tempo – O(nd).
Funciona mais ou menos assim:
- A entrada serão os números 6, 12, 44, 9
- Criaremos 10 grupos de listas (0-9), nos quais adicionaremos/classificaremos números pouco a pouco.
Próximo:
- Inicie um loop com o contador i até o número máximo de caracteres no número
- Pelo índice i da direita para a esquerda obtemos um símbolo para cada número; se não houver símbolo, então assumimos que é zero
- Converta o símbolo em um número
- Selecione um intervalo por número de índice e coloque o número inteiro lá
- Depois de terminar de pesquisar os números, converta todos os grupos novamente em uma lista de números
- Obter números classificados por classificação
- Repita até que todos os dígitos desapareçam
;
Exemplo de classificação Radix em Scala:
import scala.util.Random.nextInt
object RadixSort {
def main(args: Array[String]) = {
var maxNumber = 200
var numbersCount = 30
var maxLength = maxNumber.toString.length() - 1
var referenceNumbers = LazyList.continually(nextInt(maxNumber + 1)).take(numbersCount).toList
var numbers = referenceNumbers
var buckets = List.fill(10)(ListBuffer[Int]())
for( i <- 0 to maxLength) { numbers.foreach( number => {
var numberString = number.toString
if (numberString.length() > i) {
var index = numberString.length() - i - 1
var character = numberString.charAt(index).toString
var characterInteger = character.toInt
buckets.apply(characterInteger) += number
}
else {
buckets.apply(0) += number
}
}
)
numbers = buckets.flatten
buckets.foreach(x => x.clear())
}
println(referenceNumbers)
println(numbers)
println(s"Validation result: ${numbers == referenceNumbers.sorted}")
}
}
O algoritmo também possui uma versão para execução paralela, por exemplo em uma GPU; Há também uma opção de classificação, que deve sermuito interessante e realmente de tirar o fôlego!
Links
https://gitlab .com/demensdeum/algorithms/-/blob/master/sortAlgorithms/radixSort/radixSort.scala
Fontes
https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8F%D 0%B4%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0% BA%D0%B0
https://www.geeksforgeeks.org/radix-sort/
https://www.youtube.com/watch?v=toAlAJKojos
https://github.com/gyatskov/radix-sort
Heapsort
Heapsort – classificação em pirâmide. Complexidade de tempo do algoritmo – O (n log n), rápido, certo? Eu chamaria isso de classificação de classificação de pedras que caem. Parece-me que a maneira mais fácil de explicar é visualmente.
A entrada é uma lista de números, por exemplo:
5, 0, 7, 2, 3, 9, 4
Da esquerda para a direita, uma estrutura de dados é criada – uma árvore binária, ou como eu chamo – pirâmide. Os elementos da pirâmide podem ter no máximo dois elementos filhos, mas apenas um elemento superior.
Vamos fazer uma árvore binária:
⠀⠀5
⠀0⠀7
2 3 9 4
Se você olhar a pirâmide por muito tempo, verá que são apenas números de uma matriz, vindo um após o outro, o número de elementos em cada andar é multiplicado por dois.
A seguir, a diversão começa; vamos classificar a pirâmide de baixo para cima usando o método das pedras caindo (heapify). A classificação poderia ser iniciada a partir do último andar (2 3 9 4), mas não adianta porque não há piso abaixo onde você possa cair.
Portanto, começamos a descartar elementos do penúltimo andar (0 7)
⠀⠀5
⠀0⠀7
2 3 9 4
O primeiro elemento a cair é selecionado da direita, no nosso caso é 7, então olhamos o que está abaixo dele, e abaixo dele estão 9 e 4, nove é maior que quatro, e também nove é maior que Sete! Colocamos 7 em 9 e colocamos 9 no lugar 7.
⠀⠀5
⠀0⠀9
2 3 7 4
A seguir, entendemos que o sete não tem onde cair, passamos para o número 0, que está localizado no penúltimo andar à esquerda:
⠀⠀5
⠀0⠀9
2 3 7 4
Vamos ver o que há por baixo – 2 e 3, dois é menor que três, três é maior que zero, então trocamos zero por três:
⠀⠀5
⠀3⠀9
2 0 7 4
Quando chegar ao final do andar, vá para o andar de cima e largue tudo lá, se puder.
O resultado é uma estrutura de dados – um heap, ou seja, max heap, porque no topo está o maior elemento:
⠀⠀9
⠀3⠀7
2 0 5 4
Se você retornar para uma representação de array, você obterá uma lista:
[9, 3, 7, 2, 0, 5, 4]
A partir disso podemos concluir que ao trocar o primeiro e o último elemento, obtemos o primeiro número na posição final ordenada, ou seja, 9 deve estar no final da lista ordenada, troque de lugar:
[4, 3, 7, 2, 0, 5, 9]
Vejamos uma árvore binária:
⠀⠀4
⠀3⠀7
2 0 5 9
O resultado é uma situação em que a parte inferior da árvore está ordenada, basta colocar 4 na posição correta, repetir o algoritmo, mas não levar em consideração os números já ordenados, nomeadamente 9:
⠀⠀4
⠀3⠀7
2 0 5 9
⠀⠀7
⠀3⠀4
2 0 5 9
⠀⠀7
⠀3⠀5
2 0 4 9
Acontece que nós, tendo perdido 4, aumentamos o próximo maior número depois de 9 – 7. Troque o último número não classificado (4) e o maior número (7)
⠀⠀4
⠀3⠀5
2 0 7 9
Acontece que agora temos dois números na posição final correta:
4, 3, 5, 2, 0, 7, 9
Em seguida repetimos o algoritmo de classificação, ignorando os já classificados, no final obtemos um heap tipo:
⠀⠀0
⠀2⠀3
4 5 7 9
Ou como uma lista:
0, 2, 3, 4, 5, 7, 9
Implementação
O algoritmo geralmente é dividido em três funções:
- Criando uma pilha
- Algoritmo de peneiração (heapify)
- Substituindo o último elemento não classificado e o primeiro
O heap é criado percorrendo a penúltima linha da árvore binária usando a função heapify, da direita para a esquerda, até o final do array. A seguir no ciclo, é feita a primeira substituição de números, após a qual o primeiro elemento cai/permanece no lugar, como resultado o elemento maior cai em primeiro lugar, o ciclo é repetido com uma diminuição de participantes em um, porque após cada passagem, os números classificados permanecem no final da lista.
Exemplo de Heapsort em Ruby:
module Colors
BLUE = "\033[94m"
RED = "\033[31m"
STOP = "\033[0m"
end
def heapsort(rawNumbers)
numbers = rawNumbers.dup
def swap(numbers, from, to)
temp = numbers[from]
numbers[from] = numbers[to]
numbers[to] = temp
end
def heapify(numbers)
count = numbers.length()
lastParentNode = (count - 2) / 2
for start in lastParentNode.downto(0)
siftDown(numbers, start, count - 1)
start -= 1
end
if DEMO
puts "--- heapify ends ---"
end
end
def siftDown(numbers, start, rightBound)
cursor = start
printBinaryHeap(numbers, cursor, rightBound)
def calculateLhsChildIndex(cursor)
return cursor * 2 + 1
end
def calculateRhsChildIndex(cursor)
return cursor * 2 + 2
end
while calculateLhsChildIndex(cursor) <= rightBound
lhsChildIndex = calculateLhsChildIndex(cursor)
rhsChildIndex = calculateRhsChildIndex(cursor)
lhsNumber = numbers[lhsChildIndex]
biggerChildIndex = lhsChildIndex
if rhsChildIndex <= rightBound
rhsNumber = numbers[rhsChildIndex]
if lhsNumber < rhsNumber
biggerChildIndex = rhsChildIndex
end
end
if numbers[cursor] < numbers[biggerChildIndex]
swap(numbers, cursor, biggerChildIndex)
cursor = biggerChildIndex
else
break
end
printBinaryHeap(numbers, cursor, rightBound)
end
printBinaryHeap(numbers, cursor, rightBound)
end
def printBinaryHeap(numbers, nodeIndex = -1, rightBound = -1)
if DEMO == false
return
end
perLineWidth = (numbers.length() * 4).to_i
linesCount = Math.log2(numbers.length()).ceil()
xPrinterCount = 1
cursor = 0
spacing = 3
for y in (0..linesCount)
line = perLineWidth.times.map { " " }
spacing = spacing == 3 ? 4 : 3
printIndex = (perLineWidth / 2) - (spacing * xPrinterCount) / 2
for x in (0..xPrinterCount - 1)
if cursor >= numbers.length
break
end
if nodeIndex != -1 && cursor == nodeIndex
line[printIndex] = "%s%s%s" % [Colors::RED, numbers[cursor].to_s, Colors::STOP]
elsif rightBound != -1 && cursor > rightBound
line[printIndex] = "%s%s%s" % [Colors::BLUE, numbers[cursor].to_s, Colors::STOP]
else
line[printIndex] = numbers[cursor].to_s
end
cursor += 1
printIndex += spacing
end
print line.join()
xPrinterCount *= 2
print "\n"
end
end
heapify(numbers)
rightBound = numbers.length() - 1
while rightBound > 0
swap(numbers, 0, rightBound)
rightBound -= 1
siftDown(numbers, 0, rightBound)
end
return numbers
end
numbersCount = 14
maximalNumber = 10
numbers = numbersCount.times.map { Random.rand(maximalNumber) }
print numbers
print "\n---\n"
start = Time.now
sortedNumbers = heapsort(numbers)
finish = Time.now
heapSortTime = start - finish
start = Time.now
referenceSortedNumbers = numbers.sort()
finish = Time.now
referenceSortTime = start - finish
print "Reference sort: "
print referenceSortedNumbers
print "\n"
print "Reference sort time: %f\n" % referenceSortTime
print "Heap sort: "
print sortedNumbers
print "\n"
if DEMO == false
print "Heap sort time: %f\n" % heapSortTime
else
print "Disable DEMO for performance measure\n"
end
if sortedNumbers != referenceSortedNumbers
puts "Validation failed"
exit 1
else
puts "Validation success"
exit 0
end
Esse algoritmo não é fácil de entender sem visualização, então a primeira coisa que recomendo é escrever uma função que imprima a visualização atual da árvore binária.
Links
https://gitlab.com/demensdeum/algorithms/-/blob/master/sortAlgorithms/heapsort/heapsort.rb
Fontes
http://rosettacode.org/wiki/Sorting_algorithms/Heapsort
https://www.youtube.com/watch?v=LbB357_RwlY
https://habr.com/ru/company/ otus/blog/460087/
https://ru.wikipedia.org/wiki/Pyramid_sort
https://neerc.ifmo.ru/wiki /index.php?title=Heap_sort
https://wiki5.ru/wiki/Heapsort
https://ru.wikipedia.org/wiki/Tree (estrutura de dados)
https://ru.wikipedia.org/wiki/Heap (estrutura de dados)
https://www.youtube.com/watch?v=2DmK_H7IdTo
https://www.youtube.com/watch?v=kU4KBD4NFtw
https://www.youtube.com/watch?v=DU1uG5310x0
https://www.youtube.com/watch?v =BzQGPA_v-vc
https://www.geeksforgeeks.org/ representação de array de heap binário/
https://habr.com/ru/post/112222/
https://www.cs.usfca. edu/~galles/visualization/BST.html
https://www.youtube.com/watch?v=EQzqHWtsKq4
https://ru.wikibrief.org/wiki/Heapsort
https://www.youtube.com/watch?v=GUUpmrTnNbw
Classificação rápida
Quicksort é um algoritmo de classificação de divisão e conquista. Recursivamente, peça por peça, analisamos a matriz de números, colocando os números em ordem menor e maior a partir do elemento de referência selecionado, e inserimos o próprio elemento de referência no corte entre eles. Após várias iterações recursivas, você terá uma lista ordenada. Complexidade de tempo O(n2).
Esquema:
- Começamos obtendo uma lista de elementos externos, os limites de classificação. Na primeira etapa, os limites de classificação serão do início ao fim.
- Verifique se os limites inicial e final não se cruzam; se isso acontecer, é hora de terminar.
- Selecione algum elemento da lista e chame-o de pivô
- Mova-o para a direita até o final do último índice para que não atrapalhe
- Crie um contador de *números menores* ainda iguais a zero
- Percorrer a lista da esquerda para a direita, até e incluindo o último índice onde o elemento de referência está localizado
- Comparamos cada elemento com o de referência
- Se for menor que o de referência, trocamos de acordo com o índice do contador de números menores. Aumente o contador de números menores.
- Quando o loop atinge o elemento de suporte, paramos e trocamos o elemento de suporte pelo elemento de acordo com o contador de números menores.
- Executamos o algoritmo separadamente para a parte menor à esquerda da lista e separadamente para a parte maior à direita da lista.
- Como resultado, todas as iterações recursivas começarão a parar devido à verificação no ponto 2
- Obter uma lista ordenada
Quicksort foi inventado pelo cientista Charles Anthony Richard Hoare na Universidade Estadual de Moscou. Depois de aprender russo, ele estudou tradução computacional, bem como teoria das probabilidades na escola Kolmogorov. Em 1960, devido à crise política, deixou a União Soviética.
Exemplo de implementação em Rust:
use rand::Rng;
fn swap(numbers: &mut [i64], from: usize, to: usize) {
let temp = numbers[from];
numbers[from] = numbers[to];
numbers[to] = temp;
}
fn quicksort(numbers: &mut [i64], left: usize, right: usize) {
if left >= right {
return
}
let length = right - left;
if length <= 1 {
return
}
let pivot_index = left + (length / 2);
let pivot = numbers[pivot_index];
let last_index = right - 1;
swap(numbers, pivot_index, last_index);
let mut less_insert_index = left;
for i in left..last_index {
if numbers[i] < pivot {
swap(numbers, i, less_insert_index);
less_insert_index += 1;
}
}
swap(numbers, last_index, less_insert_index);
quicksort(numbers, left, less_insert_index);
quicksort(numbers, less_insert_index + 1, right);
}
fn main() {
let mut numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut reference_numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut rng = rand::thread_rng();
for i in 0..numbers.len() {
numbers[i] = rng.gen_range(-10..10);
reference_numbers[i] = numbers[i];
}
reference_numbers.sort();
println!("Numbers {:?}", numbers);
let length = numbers.len();
quicksort(&mut numbers, 0, length);
println!("Numbers {:?}", numbers);
println!("Reference numbers {:?}", reference_numbers);
if numbers != reference_numbers {
println!("Validation failed");
std::process::exit(1);
}
else {
println!("Validation success!");
std::process::exit(0);
}
}
Se nada estiver claro, sugiro assistir ao vídeo de Rob Edwards, da Universidade de San Diego https://www.youtube.com/watch?v=ZHVk2blR45Q mostra de maneira mais simples, passo a passo, a essência e a implementação do algoritmo.
Links
https://gitlab.com/demensdeum /algoritmos/-/tree/master/sortAlgorithms/quickSort
Fontes
https://www.youtube.com/watch?v =4s-aG6yGGLU
https://www.youtube.com/watch?v=ywWBy6J5gz8
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://ru.wikipedia.org/wiki/Быстрая_сортировка
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://www.youtube.com/watch?v=XE4VP_8Y0BU
https://www.youtube.com/watch?v=MZaf_9IZCrc
https://www.youtube.com/watch?v=ZHVk2blR45Q
http://rosettacode.org/wiki/Sorting_algorithms/Quicksort
https://www.youtube.com/watch?v=4s-aG6yGGLU
https://www.youtube.com/watch?v=dQw4w9WgXcQ
https://www.youtube.com/watch?v=maibrCbZWKw
https://www.geeksforgeeks.org/quick-sort/
https://www.youtube.com/watch?v=uXBnyYuwPe8
Classificação de inserção binária
A classificação por inserção binária é uma variante da classificação por inserção na qual a posição de inserção é determinada usando pesquisa binária. A complexidade de tempo do algoritmo é O(n2)
O algoritmo funciona assim:
- Um loop começa de zero até o final da lista
- No loop, um número é selecionado para classificação, o número é armazenado em uma variável separada
- A pesquisa binária procura o índice para inserir esse número nos números à esquerda
- Uma vez encontrado o índice, os números à esquerda são deslocados uma posição para a direita, começando no índice de inserção. No processo, o número que precisa ser classificado será apagado.
- O número salvo anteriormente é inserido no índice de inserção
- No final do loop, a lista inteira será classificada
Durante uma pesquisa binária, é possível que o número não seja encontrado e o índice não seja retornado. Devido à peculiaridade da busca binária será encontrado o número mais próximo do buscado, então para retornar o índice será necessário compará-lo com o procurado, se o procurado for menor então o procurado deverá estar em o índice à esquerda e, se for maior ou igual, à direita.
Código Go:
import (
"fmt"
"math/rand"
"time"
)
const numbersCount = 20
const maximalNumber = 100
func binarySearch(numbers []int, item int, low int, high int) int {
for high > low {
center := (low + high) / 2
if numbers[center] < item { low = center + 1 } else if numbers[center] > item {
high = center - 1
} else {
return center
}
}
if numbers[low] < item {
return low + 1
} else {
return low
}
}
func main() {
rand.Seed(time.Now().Unix())
var numbers [numbersCount]int
for i := 0; i < numbersCount; i++ {
numbers[i] = rand.Intn(maximalNumber)
}
fmt.Println(numbers)
for i := 1; i < len(numbers); i++ { searchAreaLastIndex := i - 1 insertNumber := numbers[i] insertIndex := binarySearch(numbers[:], insertNumber, 0, searchAreaLastIndex) for x := searchAreaLastIndex; x >= insertIndex; x-- {
numbers[x+1] = numbers[x]
}
numbers[insertIndex] = insertNumber
}
fmt.Println(numbers)
}
Links
Fontes
https://www.geeksforgeeks.org/binary-insertion- ordenar/
https://www.youtube.com/watch?v=-OVB5pOZJug
Classificação de casca
Shell Sort – uma variante da classificação por inserção com combinação preliminar de uma matriz de números.
Precisamos lembrar como funciona a classificação por inserção:
1. Um loop é iniciado do zero até o final do loop, assim o array é dividido em duas partes
2. Para a parte esquerda, um segundo loop é iniciado, comparando os elementos da direita para a esquerda, o elemento menor à direita é descartado até que um elemento menor à esquerda seja encontrado
3. No final de ambos os loops, obtemos uma lista ordenada
Era uma vez, o cientista da computação Donald Schell se perguntou como melhorar o algoritmo de classificação por inserção. Ele também teve a ideia de primeiro percorrer o array em dois ciclos, mas a uma certa distância, reduzindo gradativamente o “pente” até que ele se transforme em um algoritmo regular de ordenação por inserção. Tudo é realmente tão simples, sem armadilhas, aos dois ciclos acima acrescentamos outro, no qual vamos reduzindo gradativamente o tamanho do “pente”. A única coisa que você precisa fazer é verificar a distância ao comparar para que ela não ultrapasse o array.
Um tópico realmente interessante é escolher a sequência para alterar o comprimento da comparação a cada iteração do primeiro loop. É interessante porque o desempenho do algoritmo depende disso.
A tabela de opções conhecidas e complexidade de tempo pode ser encontrada aqui: https: //en.wikipedia.org/wiki/Shellsort#Gap_sequences
Pessoas diferentes estiveram envolvidas no cálculo da distância ideal, aparentemente, esse assunto era muito interessante para elas. Eles não poderiam simplesmente executar Ruby e chamar o algoritmo sort() mais rápido?
Em geral, essas pessoas estranhas escreveram dissertações sobre o tema do cálculo da distância/gap do “pente” para o algoritmo Shell. Simplesmente usei os resultados do trabalho deles e verifiquei 5 tipos de sequências, Hibbard, Knuth-Pratt, Chiura, Sedgwick.
import time
import random
from functools import reduce
import math
DEMO_MODE = False
if input("Demo Mode Y/N? ").upper() == "Y":
DEMO_MODE = True
class Colors:
BLUE = '\033[94m'
RED = '\033[31m'
END = '\033[0m'
def swap(list, lhs, rhs):
list[lhs], list[rhs] = list[rhs], list[lhs]
return list
def colorPrintoutStep(numbers: List[int], lhs: int, rhs: int):
for index, number in enumerate(numbers):
if index == lhs:
print(f"{Colors.BLUE}", end = "")
elif index == rhs:
print(f"{Colors.RED}", end = "")
print(f"{number},", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
print("\n")
input(">")
def ShellSortLoop(numbers: List[int], distanceSequence: List[int]):
distanceSequenceIterator = reversed(distanceSequence)
while distance:= next(distanceSequenceIterator, None):
for sortArea in range(0, len(numbers)):
for rhs in reversed(range(distance, sortArea + 1)):
lhs = rhs - distance
if DEMO_MODE:
print(f"Distance: {distance}")
colorPrintoutStep(numbers, lhs, rhs)
if numbers[lhs] > numbers[rhs]:
swap(numbers, lhs, rhs)
else:
break
def ShellSort(numbers: List[int]):
global ShellSequence
ShellSortLoop(numbers, ShellSequence)
def HibbardSort(numbers: List[int]):
global HibbardSequence
ShellSortLoop(numbers, HibbardSequence)
def ShellPlusKnuttPrattSort(numbers: List[int]):
global KnuttPrattSequence
ShellSortLoop(numbers, KnuttPrattSequence)
def ShellPlusCiuraSort(numbers: List[int]):
global CiuraSequence
ShellSortLoop(numbers, CiuraSequence)
def ShellPlusSedgewickSort(numbers: List[int]):
global SedgewickSequence
ShellSortLoop(numbers, SedgewickSequence)
def insertionSort(numbers: List[int]):
global insertionSortDistanceSequence
ShellSortLoop(numbers, insertionSortDistanceSequence)
def defaultSort(numbers: List[int]):
numbers.sort()
def measureExecution(inputNumbers: List[int], algorithmName: str, algorithm):
if DEMO_MODE:
print(f"{algorithmName} started")
numbers = inputNumbers.copy()
startTime = time.perf_counter()
algorithm(numbers)
endTime = time.perf_counter()
print(f"{algorithmName} performance: {endTime - startTime}")
def sortedNumbersAsString(inputNumbers: List[int], algorithm) -> str:
numbers = inputNumbers.copy()
algorithm(numbers)
return str(numbers)
if DEMO_MODE:
maximalNumber = 10
numbersCount = 10
else:
maximalNumber = 10
numbersCount = random.randint(10000, 20000)
randomNumbers = [random.randrange(1, maximalNumber) for i in range(numbersCount)]
ShellSequenceGenerator = lambda n: reduce(lambda x, _: x + [int(x[-1]/2)], range(int(math.log(numbersCount, 2))), [int(numbersCount / 2)])
ShellSequence = ShellSequenceGenerator(randomNumbers)
ShellSequence.reverse()
ShellSequence.pop()
HibbardSequence = [
0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095,
8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575,
2097151, 4194303, 8388607, 16777215, 33554431, 67108863, 134217727,
268435455, 536870911, 1073741823, 2147483647, 4294967295, 8589934591
]
KnuttPrattSequence = [
1, 4, 13, 40, 121, 364, 1093, 3280, 9841, 29524, 88573, 265720,
797161, 2391484, 7174453, 21523360, 64570081, 193710244, 581130733,
1743392200, 5230176601, 15690529804, 47071589413
]
CiuraSequence = [
1, 4, 10, 23, 57, 132, 301, 701, 1750, 4376,
10941, 27353, 68383, 170958, 427396, 1068491,
2671228, 6678071, 16695178, 41737946, 104344866,
260862166, 652155416, 1630388541
]
SedgewickSequence = [
1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905,
8929, 16001, 36289, 64769, 146305, 260609, 587521,
1045505, 2354689, 4188161, 9427969, 16764929, 37730305,
67084289, 150958081, 268386305, 603906049, 1073643521,
2415771649, 4294770689, 9663381505, 17179475969
]
insertionSortDistanceSequence = [1]
algorithms = {
"Default Python Sort": defaultSort,
"Shell Sort": ShellSort,
"Shell + Hibbard" : HibbardSort,
"Shell + Prat, Knutt": ShellPlusKnuttPrattSort,
"Shell + Ciura Sort": ShellPlusCiuraSort,
"Shell + Sedgewick Sort": ShellPlusSedgewickSort,
"Insertion Sort": insertionSort
}
for name, algorithm in algorithms.items():
measureExecution(randomNumbers, name, algorithm)
reference = sortedNumbersAsString(randomNumbers, defaultSort)
for name, algorithm in algorithms.items():
if sortedNumbersAsString(randomNumbers, algorithm) != reference:
print("Sorting validation failed")
exit(1)
print("Sorting validation success")
exit(0)
Na minha implementação, para um conjunto aleatório de números, as lacunas mais rápidas são Sedgwick e Hibbard.
meupy
Gostaria também de mencionar o analisador de tipagem estática para Python 3 – meu Deus. Ajuda a resolver os problemas inerentes às linguagens com digitação dinâmica, nomeadamente, elimina a possibilidade de colar algo onde não é necessário.
Como dizem programadores experientes, “a digitação estática não é necessária quando você tem uma equipe de profissionais”, um dia todos nos tornaremos profissionais, escreveremos código em total unidade e compreensão com as máquinas, mas por enquanto você pode usar utilitários semelhantes e linguagens de tipo estaticamente.
Links
https://gitlab.com/demensdeum /algoritmos/-/tree/master/sortAlgorithms/shellSort
http://mypy-lang.org/
Fontes
https://dl.acm.org/doi/10.1145/368370.368387
https://en.wikipedia.org/wiki/Shellsort
http://rosettacode.org/wiki/Sorting_algorithms/Shell_sort
https://ru.wikipedia.org/wiki/Сортировка_Шелла
https://neerc.ifmo.ru/wiki/index.php?title=Сортировка_Шелла
https://twitter.com/gvanrossum/status/700741601966985216
Classificação de seleção dupla
Classificação por seleção dupla – um subtipo de classificação por seleção, parece que deveria ser duas vezes mais rápido. O algoritmo vanilla faz um loop duplo pela lista de números, encontra o número mínimo e troca de lugar com o número atual apontado pelo loop no nível acima. A classificação por seleção dupla procura os números mínimo e máximo e, em seguida, substitui os dois dígitos apontados pelo loop no nível acima de – dois números à esquerda e à direita. Toda essa orgia termina quando os cursores dos números a serem substituídos são encontrados no meio da lista e, como resultado, os números ordenados são obtidos à esquerda e à direita do centro visual.
A complexidade de tempo do algoritmo é semelhante à classificação por seleção – O(n2), mas supostamente há uma aceleração de 30 %.
Estado limítrofe
Já nesta fase, você pode imaginar o momento de uma colisão, por exemplo, quando o número do cursor esquerdo (o número mínimo) aponta para o número máximo da lista, então o número mínimo é reorganizado, o rearranjo do número máximo quebra imediatamente. Portanto, todas as implementações do algoritmo contêm a verificação de tais casos e a substituição dos índices pelos corretos. Na minha implementação, uma verificação foi suficiente:
maximalNumberIndex = minimalNumberIndex;
}Реализация на Cito
Cito – язык либ, язык транслятор. На нем можно писать для C, C++, C#, Java, JavaScript, Python, Swift, TypeScript, OpenCL C, при этом совершенно ничего не зная про эти языки. Исходный код на языке Cito транслируется в исходный код на поддерживаемых языках, далее можно использовать как библиотеку, либо напрямую, исправив сгенеренный код руками. Эдакий Write once – translate to anything.
Double Selection Sort на cito:
{
public static int[] sort(int[]# numbers, int length)
{
int[]# sortedNumbers = new int[length];
for (int i = 0; i < length; i++) {
sortedNumbers[i] = numbers[i];
}
for (int leftCursor = 0; leftCursor < length / 2; leftCursor++) {
int minimalNumberIndex = leftCursor;
int minimalNumber = sortedNumbers[leftCursor];
int rightCursor = length - (leftCursor + 1);
int maximalNumberIndex = rightCursor;
int maximalNumber = sortedNumbers[maximalNumberIndex];
for (int cursor = leftCursor; cursor <= rightCursor; cursor++) { int cursorNumber = sortedNumbers[cursor]; if (minimalNumber > cursorNumber) {
minimalNumber = cursorNumber;
minimalNumberIndex = cursor;
}
if (maximalNumber < cursorNumber) {
maximalNumber = cursorNumber;
maximalNumberIndex = cursor;
}
}
if (leftCursor == maximalNumberIndex) {
maximalNumberIndex = minimalNumberIndex;
}
int fromNumber = sortedNumbers[leftCursor];
int toNumber = sortedNumbers[minimalNumberIndex];
sortedNumbers[minimalNumberIndex] = fromNumber;
sortedNumbers[leftCursor] = toNumber;
fromNumber = sortedNumbers[rightCursor];
toNumber = sortedNumbers[maximalNumberIndex];
sortedNumbers[maximalNumberIndex] = fromNumber;
sortedNumbers[rightCursor] = toNumber;
}
return sortedNumbers;
}
}
Links
https://gitlab.com/demensdeum /algoritmos/-/tree/master/sortAlgorithms/doubleSelectionSort
https://github.com/pfusik/cito
Fontes
https://www.researchgate.net/publication/330084245_Improved_Double_Selection_Sort_using_Algorithm
http://algolab.valemak.com/selection-double
https://www.geeksforgeeks.org/sorting-algorithm-slightly-improves-selection-sort/