树排序——使用二叉搜索树进行排序。时间复杂度– O(n²)。在这样的树中,左边的每个节点都有小于该节点的数字,右边的每个节点都有大于该节点的数字,当从根开始并从左到右打印值时,我们得到一个排序的数字列表。令人惊讶吧?
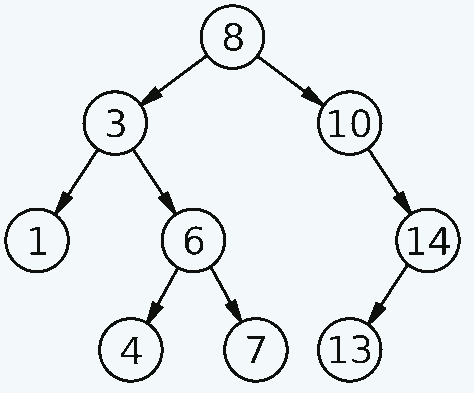
考虑二叉搜索树图:
Derrick Coetzee(公共领域)
尝试手动读取从左下角倒数第二个左侧节点开始的数字,对于左侧的每个节点 – 右侧的一个节点。
它看起来像这样:
- 左下角倒数第二个节点 – 3.
- 它有一个左分支 – 1.
- 取这个数字(1)
- 接下来我们采用顶点 3 (1, 3)
- 右侧是分支 6,但它包含分支。因此,我们以同样的方式阅读它。
- 节点 6 编号 4 的左分支 (1, 3, 4)
- 节点本身为 6 (1, 3, 4, 6)
- 右 7(1、3、4、6、7)
- 向上到根节点– 8(1,3,4,6,7,8)
- 我们以此类推将所有内容打印在右侧
- 我们得到了最终名单– 1、3、4、6、7、8、10、13、14
要在代码中实现该算法,您需要两个函数:
- 组装二叉搜索树
- 以正确的顺序打印二叉搜索树
二叉搜索树的组装方式与读取时相同,左侧或右侧的每个节点都会附加一个数字,具体取决于它是较少还是较多。
Lua 中的示例:
function Node:new(value, lhs, rhs)
output = {}
setmetatable(output, self)
self.__index = self
output.value = value
output.lhs = lhs
output.rhs = rhs
output.counter = 1
return output
end
function Node:Increment()
self.counter = self.counter + 1
end
function Node:Insert(value)
if self.lhs ~= nil and self.lhs.value > value then
self.lhs:Insert(value)
return
end
if self.rhs ~= nil and self.rhs.value < value then
self.rhs:Insert(value)
return
end
if self.value == value then
self:Increment()
return
elseif self.value > value then
if self.lhs == nil then
self.lhs = Node:new(value, nil, nil)
else
self.lhs:Insert(value)
end
return
else
if self.rhs == nil then
self.rhs = Node:new(value, nil, nil)
else
self.rhs:Insert(value)
end
return
end
end
function Node:InOrder(output)
if self.lhs ~= nil then
output = self.lhs:InOrder(output)
end
output = self:printSelf(output)
if self.rhs ~= nil then
output = self.rhs:InOrder(output)
end
return output
end
function Node:printSelf(output)
for i=0,self.counter-1 do
output = output .. tostring(self.value) .. " "
end
return output
end
function PrintArray(numbers)
output = ""
for i=0,#numbers do
output = output .. tostring(numbers[i]) .. " "
end
print(output)
end
function Treesort(numbers)
rootNode = Node:new(numbers[0], nil, nil)
for i=1,#numbers do
rootNode:Insert(numbers[i])
end
print(rootNode:InOrder(""))
end
numbersCount = 10
maxNumber = 9
numbers = {}
for i=0,numbersCount-1 do
numbers[i] = math.random(0, maxNumber)
end
PrintArray(numbers)
Treesort(numbers)Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/treesort
Источники
Convert Sorted Array to Binary Search Tree (LeetCode 108. Algorithm Explained) – YouTube
Sorting algorithms/Tree sort on a linked list – Rosetta Code
How to handle duplicates in Binary Search Tree? – GeeksforGeeks
Tree Sort | GeeksforGeeks – YouTube
桶排序
桶排序——按桶排序。该算法类似于计数排序,不同之处在于将数字收集到“桶”范围中,然后使用任何其他足够高效的排序算法对桶进行排序,最后一步是将“桶”展开减一,得到一个排序列表。
算法的时间复杂度为O(nk)。该算法在线性时间内适用于服从均匀分布规律的数据。简单来说,元素必须在一定范围内,不能有“尖峰”,例如0.0到1.0之间的数字。如果这些数字中有 4 或 999,那么根据庭院法则,这样的行不再被视为“偶数”。
Julia 中的实现示例:
buckets = Vector{Vector{Int}}()
for i in 0:bucketsCount - 1
bucket = Vector{Int}()
push!(buckets, bucket)
end
maxNumber = maximum(numbers)
for i in 0:length(numbers) - 1
bucketIndex = 1 + Int(floor(bucketsCount * numbers[1 + i] / (maxNumber + 1)))
push!(buckets[bucketIndex], numbers[1 + i])
end
for i in 0:length(buckets) - 1
bucketIndex = 1 + i
buckets[bucketIndex] = sort(buckets[bucketIndex])
end
flat = [(buckets...)...]
print(flat, "\n")
end
numbersCount = 10
maxNumber = 10
numbers = rand(1:maxNumber, numbersCount)
print(numbers,"\n")
bucketsCount = 10
bucketSort(numbers, bucketsCount)На производительность алгоритма также влияет число ведер, для большего количества чисел лучше взять большее число ведер (Algorithms in a nutshell by George T. Heineman)
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/bucketSort
Источники
https://www.youtube.com/watch?v=VuXbEb5ywrU
https://www.youtube.com/watch?v=ELrhrrCjDOA
https://medium.com/karuna-sehgal/an-introduction-to-bucket-sort-62aa5325d124
https://www.geeksforgeeks.org/bucket-sort-2/
https://ru.wikipedia.org/wiki/%D0%91%D0%BB%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0
https://www.youtube.com/watch?v=LPrF9yEKTks
https://en.wikipedia.org/wiki/Bucket_sort
https://julialang.org/
https://www.oreilly.com/library/view/algorithms-in-a/9780596516246/ch04s08.html
基数排序
Radix Sort – 基数排序。该算法与计数排序类似,不进行元素比较;而是将元素逐个字符分组到“桶”(桶)中,桶是通过当前数字字符的索引来选择的。时间复杂度– O(nd)。
它的工作原理是这样的:
- 输入为数字 6、12、44、9
- 我们将创建 10 个列表桶 (0-9),我们将在其中逐位添加/排序数字。
下一个:
- 使用计数器 i 开始循环,直到达到数字中的最大字符数
- 通过索引 i 从右到左,我们为每个数字获取一个符号;如果没有符号,则假设它为零
- 将符号转换为数字
- 按索引 – 数字选择一个存储桶,并将整个数字放在那里
- 搜索完数字后,将所有桶转换回数字列表
- 获取按排名排序的数字
- 重复直到所有数字都消失
Scala 中的基数排序示例:
import scala.util.Random.nextInt
object RadixSort {
def main(args: Array[String]) = {
var maxNumber = 200
var numbersCount = 30
var maxLength = maxNumber.toString.length() - 1
var referenceNumbers = LazyList.continually(nextInt(maxNumber + 1)).take(numbersCount).toList
var numbers = referenceNumbers
var buckets = List.fill(10)(ListBuffer[Int]())
for( i <- 0 to maxLength) { numbers.foreach( number => {
var numberString = number.toString
if (numberString.length() > i) {
var index = numberString.length() - i - 1
var character = numberString.charAt(index).toString
var characterInteger = character.toInt
buckets.apply(characterInteger) += number
}
else {
buckets.apply(0) += number
}
}
)
numbers = buckets.flatten
buckets.foreach(x => x.clear())
}
println(referenceNumbers)
println(numbers)
println(s"Validation result: ${numbers == referenceNumbers.sorted}")
}
}
该算法还有一个并行执行的版本,例如在 GPU 上;还有一个排序选项,这一定非常有趣并且真正令人惊叹!
链接
https://gitlab .com/demensdeum/algorithms/-/blob/master/sortAlgorithms/radixSort/radixSort.scala
来源
<一href="https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8F%D0% B4%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA% D0%B0"目标=“_空白” rel="noopener">https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8F%D 0%B4%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0% BA%D0%B0
https://www.geeksforgeeks.org/radix-sort/
https://www.youtube.com/watch?v=toAlAJKojos
https://github.com/gyatskov/radix-sort
堆排序
堆排序——金字塔排序。算法的时间复杂度– O(n log n),快吧?我将这种排序称为掉落卵石的排序。在我看来,最简单的解释方法就是视觉化。
输入是数字列表,例如:
5、0、7、2、3、9、4
从左到右,创建一个数据结构 – 二叉树,或者我称之为“二叉树”。金字塔。金字塔元素最多可以有两个子元素,但只能有一个顶部元素。
让我们制作一棵二叉树:
⠀⠀5
⠀0⠀7
2 3 9 4
如果你长时间观察金字塔,你会发现这些只是一个数组中的数字,一个接一个地出现,每一层的元素数量都乘以二。
接下来,有趣的事情开始了;让我们使用落下的卵石方法(heapify)对金字塔进行排序。排序可以从最后一层(2 3 9 4)开始,但是没有意义,因为下面没有任何地板可以让您跌倒。
因此,我们开始从倒数第二层(0 7)删除元素
⠀⠀5
⠀0⠀7
2 3 9 4
从右边选择第一个落下的元素,在我们的例子中是7,然后我们看看它下面的是什么,在它下面是9和4,九大于四,九也大于七!我们将 7 放到 9 上,然后将 9 提升到 7 的位置。
⠀⠀5
⠀0⠀9
2 3 7 4
接下来,我们知道七已经无处可去,我们继续看数字 0,它位于左边倒数第二层:
⠀⠀5
⠀0⠀9
2 3 7 4
让我们看看下面是什么– 2和3,二小于三,三大于零,所以我们交换零和三:
⠀⠀5
⠀3⠀9
2 0 7 4
当你到达地板的尽头时,走到上面的地板上,如果可以的话,把所有东西都扔在那里。
结果是一个数据结构——堆,即最大堆,因为顶部是最大的元素:
⠀⠀9
⠀3⠀7
2 0 5 4
如果将其返回为数组表示形式,您将得到一个列表:
[9、3、7、2、0、5、4]
由此我们可以得出结论,通过交换第一个和最后一个元素,我们得到最终排序位置的第一个数字,即 9 应该位于排序列表的末尾,交换位置:
[4、3、7、2、0、5、9]
让我们看一下二叉树:
⠀⠀4
⠀3⠀7
2 0 5 9
结果是树的下部已排序的情况,只需将 4 放到正确的位置,重复算法,但不考虑已经排序的数字,即 9:
⠀⠀4
⠀3⠀7
2 0 5 9
⠀⠀7
⠀3⠀4
2 0 5 9
⠀⠀7
⠀3⠀5
2 0 4 9
事实证明,我们在下降了 4 个数字后,又筹集了继 9 个数字之后的下一个最大数字—— 7. 交换最后一个未排序的数字(4)和最大的数字(7)
⠀⠀4
⠀3⠀5
2 0 7 9
事实证明,现在我们有两个数字处于正确的最终位置:
4、3、5、2、0、7、9
接下来我们重复排序算法,忽略已经排序的,最后我们得到一个 堆类型:
⠀⠀0
⠀2⠀3
4 5 7 9
或者作为列表:
0、2、3、4、5、7、9
实施
算法通常分为三个函数:
- 创建堆
- 筛选算法(heapify)
- 替换最后一个未排序元素和第一个元素
堆是通过使用heapify函数从右到左遍历二叉树的倒数第二行,直到数组的末尾来创建的。接下来在循环中,进行第一次数字替换,之后第一个元素落入/保持在原位,因此最大的元素落入第一位,重复该循环,参与者减少一个,因为每次传递后,排序后的数字保留在列表的末尾。
Ruby 中的堆排序示例:
module Colors
BLUE = "\033[94m"
RED = "\033[31m"
STOP = "\033[0m"
end
def heapsort(rawNumbers)
numbers = rawNumbers.dup
def swap(numbers, from, to)
temp = numbers[from]
numbers[from] = numbers[to]
numbers[to] = temp
end
def heapify(numbers)
count = numbers.length()
lastParentNode = (count - 2) / 2
for start in lastParentNode.downto(0)
siftDown(numbers, start, count - 1)
start -= 1
end
if DEMO
puts "--- heapify ends ---"
end
end
def siftDown(numbers, start, rightBound)
cursor = start
printBinaryHeap(numbers, cursor, rightBound)
def calculateLhsChildIndex(cursor)
return cursor * 2 + 1
end
def calculateRhsChildIndex(cursor)
return cursor * 2 + 2
end
while calculateLhsChildIndex(cursor) <= rightBound
lhsChildIndex = calculateLhsChildIndex(cursor)
rhsChildIndex = calculateRhsChildIndex(cursor)
lhsNumber = numbers[lhsChildIndex]
biggerChildIndex = lhsChildIndex
if rhsChildIndex <= rightBound
rhsNumber = numbers[rhsChildIndex]
if lhsNumber < rhsNumber
biggerChildIndex = rhsChildIndex
end
end
if numbers[cursor] < numbers[biggerChildIndex]
swap(numbers, cursor, biggerChildIndex)
cursor = biggerChildIndex
else
break
end
printBinaryHeap(numbers, cursor, rightBound)
end
printBinaryHeap(numbers, cursor, rightBound)
end
def printBinaryHeap(numbers, nodeIndex = -1, rightBound = -1)
if DEMO == false
return
end
perLineWidth = (numbers.length() * 4).to_i
linesCount = Math.log2(numbers.length()).ceil()
xPrinterCount = 1
cursor = 0
spacing = 3
for y in (0..linesCount)
line = perLineWidth.times.map { " " }
spacing = spacing == 3 ? 4 : 3
printIndex = (perLineWidth / 2) - (spacing * xPrinterCount) / 2
for x in (0..xPrinterCount - 1)
if cursor >= numbers.length
break
end
if nodeIndex != -1 && cursor == nodeIndex
line[printIndex] = "%s%s%s" % [Colors::RED, numbers[cursor].to_s, Colors::STOP]
elsif rightBound != -1 && cursor > rightBound
line[printIndex] = "%s%s%s" % [Colors::BLUE, numbers[cursor].to_s, Colors::STOP]
else
line[printIndex] = numbers[cursor].to_s
end
cursor += 1
printIndex += spacing
end
print line.join()
xPrinterCount *= 2
print "\n"
end
end
heapify(numbers)
rightBound = numbers.length() - 1
while rightBound > 0
swap(numbers, 0, rightBound)
rightBound -= 1
siftDown(numbers, 0, rightBound)
end
return numbers
end
numbersCount = 14
maximalNumber = 10
numbers = numbersCount.times.map { Random.rand(maximalNumber) }
print numbers
print "\n---\n"
start = Time.now
sortedNumbers = heapsort(numbers)
finish = Time.now
heapSortTime = start - finish
start = Time.now
referenceSortedNumbers = numbers.sort()
finish = Time.now
referenceSortTime = start - finish
print "Reference sort: "
print referenceSortedNumbers
print "\n"
print "Reference sort time: %f\n" % referenceSortTime
print "Heap sort: "
print sortedNumbers
print "\n"
if DEMO == false
print "Heap sort time: %f\n" % heapSortTime
else
print "Disable DEMO for performance measure\n"
end
if sortedNumbers != referenceSortedNumbers
puts "Validation failed"
exit 1
else
puts "Validation success"
exit 0
end
如果没有可视化,这个算法不容易理解,所以我建议的第一件事是编写一个函数来打印二叉树的当前视图。
链接
https://gitlab.com/demensdeum/algorithms/-/blob/master/sortAlgorithms/heapsort/heapsort.rb
来源
http://rosettacode.org/wiki/Sorting_algorithms/Heapsort
https://www.youtube.com/watch?v=LbB357_RwlY
https://habr.com/ru/company/ otus/博客/460087/
https://ru.wikipedia.org/wiki/Pyramid_sort
https://neerc.ifmo.ru/wiki /index.php?title=Heap_sort
https://wiki5.ru/wiki/Heapsort
<一href="https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_(%D1%81%D1 %82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D0%B0_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B %D1%85)" target="_blank" rel="noopener">https://ru.wikipedia.org/wiki/Tree(数据结构)
<一href="https://ru.wikipedia.org/wiki/%D0%9A%D1%83%D1%87%D0%B0_(%D1%81%D1%82%D1 %80%D1%83%D0%BA%D1%82%D1%83%D1%80%D0%B0_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85 )” target="_blank" rel="noopener">https://ru.wikipedia.org/wiki/Heap(数据结构)
https://www.youtube.com/watch?v=2DmK_H7IdTo
https://www.youtube.com/watch?v=kU4KBD4NFtw
https://www.youtube.com/watch?v=DU1uG5310x0
https://www.youtube.com/watch?v =BzQGPA_v-vc
https://www.geeksforgeeks.org/二进制堆的数组表示/
https://habr.com/ru/post/112222/
https://www.cs.usfca。 edu/~galles/visualization/BST.html
https://www.youtube.com/watch?v=EQzqHWtsKq4
<一href="https://medium.com/@dimko1/%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D1% 8B-%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B8-heapsort-796ba965018b"目标=“_空白” rel="noopener">https://medium.com/@dimko1/%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC% D1 %8B-%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B8-heapsort-796ba965018b
https://ru.wikibrief.org/wiki/Heapsort
https://www.youtube.com/watch?v=GUUpmrTnNbw
快速排序
快速排序是一种分而治之的排序算法。递归地,我们逐个解析数字数组,将所选参考元素中的数字按照较小和较大的顺序放置,并将参考元素本身插入到它们之间的截止位置。经过几次递归迭代后,您将得到一个排序列表。时间复杂度 O(n2)。
方案:
- 我们首先从外部获取元素列表,即排序边界。第一步,排序边界将从头到尾。
- 检查起始边界和结束边界是否相交;如果发生这种情况,则该结束了
- 从列表中选择某个元素并将其命名为数据透视
- 将其向右移动到最后一个索引处的末尾,这样就不会妨碍
- 创建一个*较小数字*仍等于零的计数器
- 从左到右循环遍历列表,直到引用元素所在的最后一个索引(包括该索引)
- 我们将每个元素与参考元素进行比较
- 如果小于参考值,则根据较小数字的计数器的索引进行交换。增加较小数字的计数器。
- 当循环到达支持元素时,我们停止并根据较小数字的计数器将支持元素与元素交换。
- 我们分别针对列表左侧较小的部分和列表右侧较大的部分分别运行该算法。
- 因此,由于检查点 2,所有递归迭代都将开始停止
- 获取排序列表
快速排序是由莫斯科国立大学的科学家 Charles Anthony Richard Hoare 发明的,他在学习俄语后,在 Kolmogorov 学院学习了计算机翻译以及概率论。 1960年,因政治危机离开苏联。
Rust 中的示例实现:
use rand::Rng;
fn swap(numbers: &mut [i64], from: usize, to: usize) {
let temp = numbers[from];
numbers[from] = numbers[to];
numbers[to] = temp;
}
fn quicksort(numbers: &mut [i64], left: usize, right: usize) {
if left >= right {
return
}
let length = right - left;
if length <= 1 {
return
}
let pivot_index = left + (length / 2);
let pivot = numbers[pivot_index];
let last_index = right - 1;
swap(numbers, pivot_index, last_index);
let mut less_insert_index = left;
for i in left..last_index {
if numbers[i] < pivot {
swap(numbers, i, less_insert_index);
less_insert_index += 1;
}
}
swap(numbers, last_index, less_insert_index);
quicksort(numbers, left, less_insert_index);
quicksort(numbers, less_insert_index + 1, right);
}
fn main() {
let mut numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut reference_numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut rng = rand::thread_rng();
for i in 0..numbers.len() {
numbers[i] = rng.gen_range(-10..10);
reference_numbers[i] = numbers[i];
}
reference_numbers.sort();
println!("Numbers {:?}", numbers);
let length = numbers.len();
quicksort(&mut numbers, 0, length);
println!("Numbers {:?}", numbers);
println!("Reference numbers {:?}", reference_numbers);
if numbers != reference_numbers {
println!("Validation failed");
std::process::exit(1);
}
else {
println!("Validation success!");
std::process::exit(0);
}
}
如果不清楚,我建议观看圣地亚哥大学 Rob Edwards 的视频 https://www.youtube.com/watch?v=ZHVk2blR45Q 最简单、一步步展示了算法的本质和实现。
链接
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/quickSort
来源
https://www.youtube.com/watch?v =4s-aG6yGGLU
https://www.youtube.com/watch?v=ywWBy6J5gz8
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://ru.wikipedia.org/wiki/Быстрая_сортировка
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://www.youtube.com/watch?v=XE4VP_8Y0BU
https://www.youtube.com/watch?v=MZaf_9IZCrc
https://www.youtube.com/watch?v=ZHVk2blR45Q
http://rosettacode.org/wiki/Sorting_algorithms/Quicksort
https://www.youtube.com/watch?v=4s-aG6yGGLU
https://www.youtube.com/watch?v=dQw4w9WgXcQ
https://www.youtube.com/watch?v=maibrCbZWKw
https://www.geeksforgeeks.org/quick-sort/
https://www.youtube.com/watch?v=uXBnyYuwPe8
二元插入排序
二分插入排序是插入排序的一种变体,其中使用二分查找来确定插入位置。该算法的时间复杂度为O(n2)
该算法的工作原理如下:
- 循环从零开始到列表末尾
- 在循环中选择一个数字进行排序,该数字存储在单独的变量中
- 二分查找查找索引以将此数字插入左侧的数字
- 一旦找到索引,左侧的数字就会从插入索引开始向右移动一位。在此过程中,需要排序的数字将被删除。
- 之前保存的号码将插入到插入索引处
- 循环结束时,整个列表将被排序
在二分查找过程中,有可能找不到该数字并且不会返回索引。由于二分查找的特殊性,会找到与要查找的数字最接近的数字,然后要返回索引,需要将其与要查找的数字进行比较,如果要查找的数字较小,则要返回的索引应为左侧的索引,如果大于或等于右侧的索引。
执行代码:
import (
"fmt"
"math/rand"
"time"
)
const numbersCount = 20
const maximalNumber = 100
func binarySearch(numbers []int, item int, low int, high int) int {
for high > low {
center := (low + high) / 2
if numbers[center] < item { low = center + 1 } else if numbers[center] > item {
high = center - 1
} else {
return center
}
}
if numbers[low] < item {
return low + 1
} else {
return low
}
}
func main() {
rand.Seed(time.Now().Unix())
var numbers [numbersCount]int
for i := 0; i < numbersCount; i++ {
numbers[i] = rand.Intn(maximalNumber)
}
fmt.Println(numbers)
for i := 1; i < len(numbers); i++ { searchAreaLastIndex := i - 1 insertNumber := numbers[i] insertIndex := binarySearch(numbers[:], insertNumber, 0, searchAreaLastIndex) for x := searchAreaLastIndex; x >= insertIndex; x-- {
numbers[x+1] = numbers[x]
}
numbers[insertIndex] = insertNumber
}
fmt.Println(numbers)
}
链接
来源
https://www.geeksforgeeks.org/binary-insertion-排序/
https://www.youtube.com/watch?v=-OVB5pOZJug
希尔排序
希尔排序 – 插入排序的一种变体,对数字数组进行初步组合。
我们需要记住插入排序是如何工作的:
1.一个循环从零开始到循环结束,因此数组被分成两部分
2. 对于左侧部分,启动第二个循环,从右到左比较元素,删除右侧较小的元素,直到找到左侧较小的元素
3. 在两个循环结束时,我们得到一个排序列表
很久以前,计算机科学家 Donald Schell 想知道如何改进插入排序算法。他还想出了这样的想法:首先分两个周期遍历数组,但在一定距离内,逐渐减少“梳子”,直到变成常规的插入排序算法。一切真的就是这么简单,没有陷阱,在上面的两个循环中我们添加了另一个循环,在这个循环中我们逐渐减小了“梳子”的尺寸。您唯一需要做的就是在比较时检查距离,使其不会超出数组。
一个真正有趣的主题是选择用于更改第一个循环每次迭代的比较长度的序列。有趣的是,算法的性能取决于它。
已知选项和时间复杂度表可以在这里找到:https: //en .wikipedia.org/wiki/Shellsort#Gap_sequences
不同的人参与计算理想距离;显然,这个话题对他们来说很有趣。他们不能只运行 Ruby 并调用最快的 sort() 算法吗?
总的来说,这些奇怪的人写的论文主题是计算 Shell 算法的“梳子”的距离/间隙。我简单地使用了他们的工作结果并检查了 5 种类型的序列:Hibbard、Knuth-Pratt、Chiura、Sedgwick。
import time
import random
from functools import reduce
import math
DEMO_MODE = False
if input("Demo Mode Y/N? ").upper() == "Y":
DEMO_MODE = True
class Colors:
BLUE = '\033[94m'
RED = '\033[31m'
END = '\033[0m'
def swap(list, lhs, rhs):
list[lhs], list[rhs] = list[rhs], list[lhs]
return list
def colorPrintoutStep(numbers: List[int], lhs: int, rhs: int):
for index, number in enumerate(numbers):
if index == lhs:
print(f"{Colors.BLUE}", end = "")
elif index == rhs:
print(f"{Colors.RED}", end = "")
print(f"{number},", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
print("\n")
input(">")
def ShellSortLoop(numbers: List[int], distanceSequence: List[int]):
distanceSequenceIterator = reversed(distanceSequence)
while distance:= next(distanceSequenceIterator, None):
for sortArea in range(0, len(numbers)):
for rhs in reversed(range(distance, sortArea + 1)):
lhs = rhs - distance
if DEMO_MODE:
print(f"Distance: {distance}")
colorPrintoutStep(numbers, lhs, rhs)
if numbers[lhs] > numbers[rhs]:
swap(numbers, lhs, rhs)
else:
break
def ShellSort(numbers: List[int]):
global ShellSequence
ShellSortLoop(numbers, ShellSequence)
def HibbardSort(numbers: List[int]):
global HibbardSequence
ShellSortLoop(numbers, HibbardSequence)
def ShellPlusKnuttPrattSort(numbers: List[int]):
global KnuttPrattSequence
ShellSortLoop(numbers, KnuttPrattSequence)
def ShellPlusCiuraSort(numbers: List[int]):
global CiuraSequence
ShellSortLoop(numbers, CiuraSequence)
def ShellPlusSedgewickSort(numbers: List[int]):
global SedgewickSequence
ShellSortLoop(numbers, SedgewickSequence)
def insertionSort(numbers: List[int]):
global insertionSortDistanceSequence
ShellSortLoop(numbers, insertionSortDistanceSequence)
def defaultSort(numbers: List[int]):
numbers.sort()
def measureExecution(inputNumbers: List[int], algorithmName: str, algorithm):
if DEMO_MODE:
print(f"{algorithmName} started")
numbers = inputNumbers.copy()
startTime = time.perf_counter()
algorithm(numbers)
endTime = time.perf_counter()
print(f"{algorithmName} performance: {endTime - startTime}")
def sortedNumbersAsString(inputNumbers: List[int], algorithm) -> str:
numbers = inputNumbers.copy()
algorithm(numbers)
return str(numbers)
if DEMO_MODE:
maximalNumber = 10
numbersCount = 10
else:
maximalNumber = 10
numbersCount = random.randint(10000, 20000)
randomNumbers = [random.randrange(1, maximalNumber) for i in range(numbersCount)]
ShellSequenceGenerator = lambda n: reduce(lambda x, _: x + [int(x[-1]/2)], range(int(math.log(numbersCount, 2))), [int(numbersCount / 2)])
ShellSequence = ShellSequenceGenerator(randomNumbers)
ShellSequence.reverse()
ShellSequence.pop()
HibbardSequence = [
0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095,
8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575,
2097151, 4194303, 8388607, 16777215, 33554431, 67108863, 134217727,
268435455, 536870911, 1073741823, 2147483647, 4294967295, 8589934591
]
KnuttPrattSequence = [
1, 4, 13, 40, 121, 364, 1093, 3280, 9841, 29524, 88573, 265720,
797161, 2391484, 7174453, 21523360, 64570081, 193710244, 581130733,
1743392200, 5230176601, 15690529804, 47071589413
]
CiuraSequence = [
1, 4, 10, 23, 57, 132, 301, 701, 1750, 4376,
10941, 27353, 68383, 170958, 427396, 1068491,
2671228, 6678071, 16695178, 41737946, 104344866,
260862166, 652155416, 1630388541
]
SedgewickSequence = [
1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905,
8929, 16001, 36289, 64769, 146305, 260609, 587521,
1045505, 2354689, 4188161, 9427969, 16764929, 37730305,
67084289, 150958081, 268386305, 603906049, 1073643521,
2415771649, 4294770689, 9663381505, 17179475969
]
insertionSortDistanceSequence = [1]
algorithms = {
"Default Python Sort": defaultSort,
"Shell Sort": ShellSort,
"Shell + Hibbard" : HibbardSort,
"Shell + Prat, Knutt": ShellPlusKnuttPrattSort,
"Shell + Ciura Sort": ShellPlusCiuraSort,
"Shell + Sedgewick Sort": ShellPlusSedgewickSort,
"Insertion Sort": insertionSort
}
for name, algorithm in algorithms.items():
measureExecution(randomNumbers, name, algorithm)
reference = sortedNumbersAsString(randomNumbers, defaultSort)
for name, algorithm in algorithms.items():
if sortedNumbersAsString(randomNumbers, algorithm) != reference:
print("Sorting validation failed")
exit(1)
print("Sorting validation success")
exit(0)
在我的实现中,对于一组随机数字,最快的差距是 Sedgwick 和 Hibbard。
mypy
我还想提一下 Python 3 的静态类型分析器——我的。有助于解决动态类型语言固有的问题,即它消除了将某些内容粘贴在不需要的地方的可能性。
正如经验丰富的程序员所说,“当你拥有一支专业团队时,就不需要静态类型”,有一天我们都会成为专业人士,我们将编写与机器完全统一和理解的代码,但现在您可以使用类似的实用程序和静态类型语言。
链接
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/shellSort
http://mypy-lang.org/
来源
https://dl.acm.org/doi/10.1145/368370.368387
https://en.wikipedia.org/wiki/Shellsort
http://rosettacode.org/wiki/Sorting_algorithms/Shell_sort
https://ru.wikipedia.org/wiki/Сортировка_Шелла
https://neerc.ifmo.ru/wiki/index.php?title=Сортировка_Шелла
https://twitter.com/gvanrossum/status/700741601966985216
双选排序
双选择排序 – 选择排序的子类型,看起来它的速度应该是它的两倍。普通算法对数字列表进行双重循环,找到最小数字并与上一层循环指向的当前数字交换位置。双选择排序查找最小和最大数字,然后替换上一层循环所指向的两位数字。左边和右边两个数字。当在列表中间找到需要替换的数字的光标时,整个狂欢就结束了,这样,视觉中心左右就得到了排序后的数字。
该算法的时间复杂度类似于选择排序– O(n2),但据说加速度为 30 %。
边缘状态
已经到了这个阶段,你可以想象一下碰撞的瞬间,比如当左光标的数字(最小的数字)指向列表中的最大的数字,那么最小的数字重新排列,重新排列最大数量的立即崩溃。因此,该算法的所有实现都包含检查此类情况并用正确的索引替换索引。在我的实现中,一次检查就足够了:
maximalNumberIndex = minimalNumberIndex;
}Реализация на Cito
Cito – язык либ, язык транслятор. На нем можно писать для C, C++, C#, Java, JavaScript, Python, Swift, TypeScript, OpenCL C, при этом совершенно ничего не зная про эти языки. Исходный код на языке Cito транслируется в исходный код на поддерживаемых языках, далее можно использовать как библиотеку, либо напрямую, исправив сгенеренный код руками. Эдакий Write once – translate to anything.
Double Selection Sort на cito:
{
public static int[] sort(int[]# numbers, int length)
{
int[]# sortedNumbers = new int[length];
for (int i = 0; i < length; i++) {
sortedNumbers[i] = numbers[i];
}
for (int leftCursor = 0; leftCursor < length / 2; leftCursor++) {
int minimalNumberIndex = leftCursor;
int minimalNumber = sortedNumbers[leftCursor];
int rightCursor = length - (leftCursor + 1);
int maximalNumberIndex = rightCursor;
int maximalNumber = sortedNumbers[maximalNumberIndex];
for (int cursor = leftCursor; cursor <= rightCursor; cursor++) { int cursorNumber = sortedNumbers[cursor]; if (minimalNumber > cursorNumber) {
minimalNumber = cursorNumber;
minimalNumberIndex = cursor;
}
if (maximalNumber < cursorNumber) {
maximalNumber = cursorNumber;
maximalNumberIndex = cursor;
}
}
if (leftCursor == maximalNumberIndex) {
maximalNumberIndex = minimalNumberIndex;
}
int fromNumber = sortedNumbers[leftCursor];
int toNumber = sortedNumbers[minimalNumberIndex];
sortedNumbers[minimalNumberIndex] = fromNumber;
sortedNumbers[leftCursor] = toNumber;
fromNumber = sortedNumbers[rightCursor];
toNumber = sortedNumbers[maximalNumberIndex];
sortedNumbers[maximalNumberIndex] = fromNumber;
sortedNumbers[rightCursor] = toNumber;
}
return sortedNumbers;
}
}
链接
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/doubleSelectionSort
https://github.com/pfusik/cito
来源
https://www.researchgate.net/publication/330084245_Improved_Double_Selection_Sort_using_Algorithm
http://algolab.valemak.com/selection-double
https://www.geeksforgeeks.org/sorting-algorithm-slightly-improves-selection-sort/