Tree sort – сортировка двоичным деревом поиска. Временная сложность – O(n²). В таком дереве у каждой ноды слева числа меньше ноды, справа больше ноды, при приходе от корня и распечатке значений слева направо, получаем отсортированный список чисел. Удивительно да?
Рассмотрим схему двоичного дерева поиска:
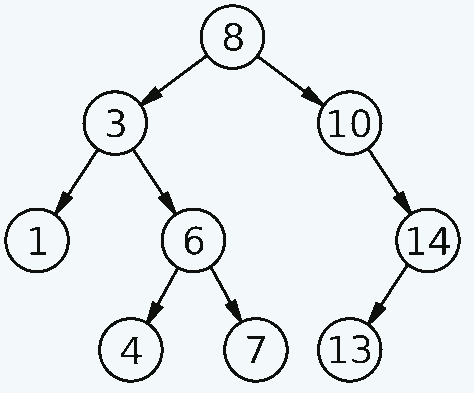
Derrick Coetzee (public domain)
Попробуйте вручную прочитать числа начиная с предпоследней левой ноды нижнего левого угла, для каждой ноды слева – нода – справа.
Получится так:
- Предпоследняя нода слева внизу – 3.
- У нее есть левая ветвь – 1.
- Берем это число (1)
- Дальше берем саму вершину 3 (1, 3)
- Справа ветвь 6, но она содержит ветви. Поэтому ее прочитываем таким же образом.
- CЛева ветвь ноды 6 число 4 (1, 3, 4)
- Сама нода 6 (1, 3, 4, 6)
- Справа 7 (1, 3, 4, 6, 7)
- Идем наверх к корневой ноде – 8 (1,3, 4 ,6, 7, 8)
- Печатаем все что справа по аналогии
- Получаем итоговый список – 1, 3, 4, 6, 7, 8, 10, 13, 14
Чтобы реализовать алгоритм в коде потребуются две функции:
- Сборка бинарного дерева поиска
- Распечатка бинарного дерева поиска в правильно порядке
Собирают бинарное древо поиска также как и прочитывают, к каждой ноде прицепляется число слева или справа, в зависимости от того – меньше оно или больше.
Пример на Lua:
Node = {value = nil, lhs = nil, rhs = nil}
function Node:new(value, lhs, rhs)
output = {}
setmetatable(output, self)
self.__index = self
output.value = value
output.lhs = lhs
output.rhs = rhs
output.counter = 1
return output
end
function Node:Increment()
self.counter = self.counter + 1
end
function Node:Insert(value)
if self.lhs ~= nil and self.lhs.value > value then
self.lhs:Insert(value)
return
end
if self.rhs ~= nil and self.rhs.value < value then
self.rhs:Insert(value)
return
end
if self.value == value then
self:Increment()
return
elseif self.value > value then
if self.lhs == nil then
self.lhs = Node:new(value, nil, nil)
else
self.lhs:Insert(value)
end
return
else
if self.rhs == nil then
self.rhs = Node:new(value, nil, nil)
else
self.rhs:Insert(value)
end
return
end
end
function Node:InOrder(output)
if self.lhs ~= nil then
output = self.lhs:InOrder(output)
end
output = self:printSelf(output)
if self.rhs ~= nil then
output = self.rhs:InOrder(output)
end
return output
end
function Node:printSelf(output)
for i=0,self.counter-1 do
output = output .. tostring(self.value) .. " "
end
return output
end
function PrintArray(numbers)
output = ""
for i=0,#numbers do
output = output .. tostring(numbers[i]) .. " "
end
print(output)
end
function Treesort(numbers)
rootNode = Node:new(numbers[0], nil, nil)
for i=1,#numbers do
rootNode:Insert(numbers[i])
end
print(rootNode:InOrder(""))
end
numbersCount = 10
maxNumber = 9
numbers = {}
for i=0,numbersCount-1 do
numbers[i] = math.random(0, maxNumber)
end
PrintArray(numbers)
Treesort(numbers)Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/treesort
Источники
Convert Sorted Array to Binary Search Tree (LeetCode 108. Algorithm Explained) – YouTube
Sorting algorithms/Tree sort on a linked list – Rosetta Code
How to handle duplicates in Binary Search Tree? – GeeksforGeeks
Tree Sort | GeeksforGeeks – YouTube