Tri par arbre : tri à l’aide d’un arbre de recherche binaire. Complexité temporelle – O(n²). Dans un tel arbre, chaque nœud à gauche a des nombres inférieurs au nœud, à droite il y en a plus que le nœud, en venant de la racine et en imprimant les valeurs de gauche à droite, on obtient une liste triée de nombres . Surprenant, non ?
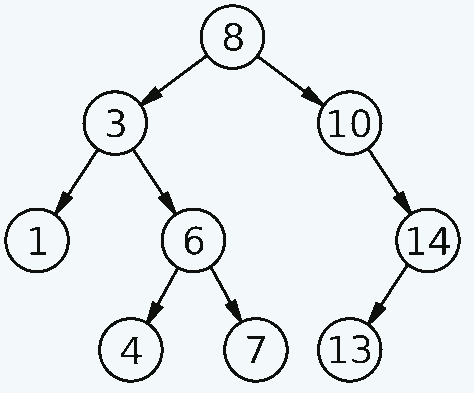
Considérez l’arbre de recherche binaire :
Derrick Coetzee (domaine public)
Essayez de lire manuellement les nombres en partant de l’avant-dernier nœud gauche du coin inférieur gauche, pour chaque nœud à gauche – un nœud – à droite.
Cela ressemblera à ceci :
- Avant-dernier nœud en bas à gauche – 3.
- Il a une branche gauche – 1.
- Prenez ce numéro (1)
- Ensuite, nous prenons le sommet 3 (1, 3)
- À droite se trouve la branche 6, mais elle contient des branches. Par conséquent, nous le lisons de la même manière.
- Branche gauche du nœud 6 numéro 4 (1, 3, 4)
- Le nœud lui-même est 6 (1, 3, 4, 6)
- Droite 7 (1, 3, 4, 6, 7)
- Montez jusqu’au nœud racine – 8 (1,3, 4,6, 7, 8)
- Nous imprimons tout à droite par analogie
- Nous obtenons la liste finale – 1, 3, 4, 6, 7, 8, 10, 13, 14
Pour implémenter l’algorithme dans le code, vous aurez besoin de deux fonctions :
- Assembler un arbre de recherche binaire
- Imprimer l’arbre de recherche binaire dans le bon ordre
L’arbre binaire de recherche est assemblé de la même manière qu’il est lu, un numéro est attaché à chaque nœud à gauche ou à droite, selon qu’il est inférieur ou supérieur.
Exemple en Lua :
function Node:new(value, lhs, rhs)
output = {}
setmetatable(output, self)
self.__index = self
output.value = value
output.lhs = lhs
output.rhs = rhs
output.counter = 1
return output
end
function Node:Increment()
self.counter = self.counter + 1
end
function Node:Insert(value)
if self.lhs ~= nil and self.lhs.value > value then
self.lhs:Insert(value)
return
end
if self.rhs ~= nil and self.rhs.value < value then
self.rhs:Insert(value)
return
end
if self.value == value then
self:Increment()
return
elseif self.value > value then
if self.lhs == nil then
self.lhs = Node:new(value, nil, nil)
else
self.lhs:Insert(value)
end
return
else
if self.rhs == nil then
self.rhs = Node:new(value, nil, nil)
else
self.rhs:Insert(value)
end
return
end
end
function Node:InOrder(output)
if self.lhs ~= nil then
output = self.lhs:InOrder(output)
end
output = self:printSelf(output)
if self.rhs ~= nil then
output = self.rhs:InOrder(output)
end
return output
end
function Node:printSelf(output)
for i=0,self.counter-1 do
output = output .. tostring(self.value) .. " "
end
return output
end
function PrintArray(numbers)
output = ""
for i=0,#numbers do
output = output .. tostring(numbers[i]) .. " "
end
print(output)
end
function Treesort(numbers)
rootNode = Node:new(numbers[0], nil, nil)
for i=1,#numbers do
rootNode:Insert(numbers[i])
end
print(rootNode:InOrder(""))
end
numbersCount = 10
maxNumber = 9
numbers = {}
for i=0,numbersCount-1 do
numbers[i] = math.random(0, maxNumber)
end
PrintArray(numbers)
Treesort(numbers)Важный нюанс что для чисел которые равны вершине придумано множество интересных механизмов подцепления к ноде, я же просто добавил счетчик к классу вершины, при распечатке числа возвращаются по счетчику.
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/treesort
Источники
Convert Sorted Array to Binary Search Tree (LeetCode 108. Algorithm Explained) – YouTube
Sorting algorithms/Tree sort on a linked list – Rosetta Code
How to handle duplicates in Binary Search Tree? – GeeksforGeeks
Tree Sort | GeeksforGeeks – YouTube
Tri par seau
Tri par seaux : tri par seaux. L’algorithme est similaire au tri par comptage, à la différence que les nombres sont collectés dans des plages de « seaux », puis les seaux sont triés à l’aide de tout autre algorithme de tri suffisamment productif, et l’étape finale consiste à déplier les « seaux » par un, ce qui donne une liste triée
La complexité temporelle de l’algorithme est O(nk). L’algorithme fonctionne en temps linéaire pour des données obéissant à une loi de distribution uniforme. Pour faire simple, les éléments doivent être dans une certaine plage, sans « pointes », par exemple des nombres de 0,0 à 1,0. Si parmi ces nombres il y en a 4 ou 999, alors selon les lois de la cour, une telle rangée n’est plus considérée comme « paire ».
Exemple d’implémentation dans Julia :
buckets = Vector{Vector{Int}}()
for i in 0:bucketsCount - 1
bucket = Vector{Int}()
push!(buckets, bucket)
end
maxNumber = maximum(numbers)
for i in 0:length(numbers) - 1
bucketIndex = 1 + Int(floor(bucketsCount * numbers[1 + i] / (maxNumber + 1)))
push!(buckets[bucketIndex], numbers[1 + i])
end
for i in 0:length(buckets) - 1
bucketIndex = 1 + i
buckets[bucketIndex] = sort(buckets[bucketIndex])
end
flat = [(buckets...)...]
print(flat, "\n")
end
numbersCount = 10
maxNumber = 10
numbers = rand(1:maxNumber, numbersCount)
print(numbers,"\n")
bucketsCount = 10
bucketSort(numbers, bucketsCount)На производительность алгоритма также влияет число ведер, для большего количества чисел лучше взять большее число ведер (Algorithms in a nutshell by George T. Heineman)
Ссылки
https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/bucketSort
Источники
https://www.youtube.com/watch?v=VuXbEb5ywrU
https://www.youtube.com/watch?v=ELrhrrCjDOA
https://medium.com/karuna-sehgal/an-introduction-to-bucket-sort-62aa5325d124
https://www.geeksforgeeks.org/bucket-sort-2/
https://ru.wikipedia.org/wiki/%D0%91%D0%BB%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0
https://www.youtube.com/watch?v=LPrF9yEKTks
https://en.wikipedia.org/wiki/Bucket_sort
https://julialang.org/
https://www.oreilly.com/library/view/algorithms-in-a/9780596516246/ch04s08.html
Tri par base
Tri Radix – tri par base. L’algorithme est similaire au tri par comptage dans la mesure où il n’y a pas de comparaison des éléments ; à la place, les éléments sont regroupés *caractère par caractère* dans des *buckets* (buckets), le bucket est sélectionné par l’index du numéro-caractère actuel. Complexité temporelle – O(nd).
Cela fonctionne comme ceci :
- L’entrée sera les nombres 6, 12, 44, 9
- Nous allons créer 10 groupes de listes (0 à 9), dans lesquels nous ajouterons/trierons des nombres petit à petit.
Suivant :
- Démarrer une boucle avec le compteur i jusqu’au nombre maximum de caractères du nombre
- Par l’index i de droite à gauche, nous obtenons un symbole pour chaque nombre ; s’il n’y a pas de symbole, alors nous supposons qu’il est nul
- Convertir le symbole en nombre
- Sélectionnez un bucket par numéro d’index et insérez-y le numéro entier
- Après avoir terminé la recherche parmi les nombres, reconvertissez tous les compartiments en une liste de nombres
- Obtenir des chiffres triés par rang
- Répétez jusqu’à ce que tous les chiffres aient disparu
Exemple de tri Radix dans Scala :
import scala.util.Random.nextInt
object RadixSort {
def main(args: Array[String]) = {
var maxNumber = 200
var numbersCount = 30
var maxLength = maxNumber.toString.length() - 1
var referenceNumbers = LazyList.continually(nextInt(maxNumber + 1)).take(numbersCount).toList
var numbers = referenceNumbers
var buckets = List.fill(10)(ListBuffer[Int]())
for( i <- 0 to maxLength) { numbers.foreach( number => {
var numberString = number.toString
if (numberString.length() > i) {
var index = numberString.length() - i - 1
var character = numberString.charAt(index).toString
var characterInteger = character.toInt
buckets.apply(characterInteger) += number
}
else {
buckets.apply(0) += number
}
}
)
numbers = buckets.flatten
buckets.foreach(x => x.clear())
}
println(referenceNumbers)
println(numbers)
println(s"Validation result: ${numbers == referenceNumbers.sorted}")
}
}
L’algorithme dispose également d’une version pour une exécution parallèle, par exemple sur un GPU ; Il y a aussi une petite option de tri, qui doit êtretrès intéressante et vraiment époustouflante !
Liens
https://gitlab .com/demensdeum/algorithms/-/blob/master/sortAlgorithms/radixSort/radixSort.scala
Sources
https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8F%D 0%B4%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0% BA%D0%B0
https://www.geeksforgeeks.org/radix-sort/
https://www.youtube.com/watch?v=toAlAJKojos
https://github.com/gyatskov/radix-sort
Tri en tas
Heapsort – tri pyramidal. Complexité temporelle de l’algorithme – O(n log n), vite, non ? J’appellerais ce tri le tri des cailloux qui tombent. Il me semble que la façon la plus simple de l’expliquer est visuellement.
L’entrée est une liste de nombres, par exemple :
5, 0, 7, 2, 3, 9, 4
De gauche à droite, une structure de données est créée : un arbre binaire, ou comme je l’appelle : un arbre binaire. pyramide. Les éléments pyramidaux peuvent avoir un maximum de deux éléments enfants, mais un seul élément supérieur.
Créons un arbre binaire :
⠀⠀5
⠀0⠀7
2 3 9 4
Si vous regardez la pyramide pendant longtemps, vous pouvez voir que ce ne sont que des nombres provenant d’un tableau, se succédant les uns après les autres, le nombre d’éléments dans chaque étage est multiplié par deux.
Ensuite, le plaisir commence : trions la pyramide de bas en haut en utilisant la méthode des cailloux tombants (tassifier). Le tri pourrait être lancé depuis le dernier étage (2 3 9 4), mais cela ne sert à rien car il n’y a pas d’étage en dessous où vous pourriez tomber.
Par conséquent, nous commençons à supprimer les éléments de l’avant-dernier étage (0 7)
⠀⠀5
⠀0⠀7
2 3 9 4
Le premier élément à tomber est sélectionné à droite, dans notre cas c’est 7, puis nous regardons ce qu’il y a en dessous, et en dessous se trouvent 9 et 4, neuf est supérieur à quatre, et neuf est également supérieur à Sept! Nous déposons 7 sur 9 et soulevons 9 à la place 7.
⠀⠀5
⠀0⠀9
2 3 7 4
Ensuite, on comprend que sept n’a nulle part où descendre plus bas, on passe au chiffre 0, qui se situe à l’avant-dernier étage à gauche :
⠀⠀5
⠀0⠀9
2 3 7 4
Voyons ce qu’il y a en dessous – 2 et 3, deux est inférieur à trois, trois est supérieur à zéro, donc on échange zéro et trois :
⠀⠀5
⠀3⠀9
2 0 7 4
Lorsque vous atteignez le bout de l’étage, allez à l’étage supérieur et déposez tout là-bas si vous le pouvez.
Le résultat est une structure de données – un tas, à savoir max tas, car en haut se trouve le plus grand élément :
⠀⠀9
⠀3⠀7
2 0 5 4
Si vous le renvoyez à une représentation matricielle, vous obtenez une liste :
[9, 3, 7, 2, 0, 5, 4]
De là, nous pouvons conclure qu’en échangeant le premier et le dernier élément, nous obtenons le premier nombre dans la position triée finale, à savoir que 9 doit être à la fin de la liste triée, échangez les places :
[4, 3, 7, 2, 0, 5, 9]
Regardons un arbre binaire :
⠀⠀4
⠀3⠀7
2 0 5 9
Le résultat est une situation dans laquelle la partie inférieure de l’arbre est triée, il suffit d’en déposer 4 à la bonne position, de répéter l’algorithme, mais de ne pas prendre en compte les nombres déjà triés, à savoir 9 :
⠀⠀4
⠀3⠀7
2 0 5 9
⠀⠀7
⠀3⠀4
2 0 5 9
⠀⠀7
⠀3⠀5
2 0 4 9
Il s’est avéré que nous, après avoir perdu 4, avons soulevé le deuxième plus grand nombre après 9 – 7. Échangez le dernier numéro non trié (4) et le plus grand nombre (7)
⠀⠀4
⠀3⠀5
2 0 7 9
Il s’avère que nous avons maintenant deux nombres dans la bonne position finale :
4, 3, 5, 2, 0, 7, 9
Ensuite, nous répétons l’algorithme de tri, en ignorant ceux déjà triés, à la fin nous obtenons un tas :
⠀⠀0
⠀2⠀3
4 5 7 9
Ou sous forme de liste :
0, 2, 3, 4, 5, 7, 9
Mise en œuvre
L’algorithme est généralement divisé en trois fonctions :
- Créer un tas
- Algorithme de tamisage (heapify)
- Remplacement du dernier élément non trié et du premier
Le tas est créé en parcourant l’avant-dernière ligne de l’arbre binaire à l’aide de la fonction heapify, de droite à gauche, jusqu’à la fin du tableau. Ensuite dans le cycle, le premier remplacement des nombres est effectué, après quoi le premier élément tombe/reste en place, à la suite de quoi le plus grand élément tombe à la première place, le cycle se répète avec une diminution du nombre de participants d’un, car après chaque passage, les nombres triés restent à la fin de la liste.
Exemple de tri par tas dans Ruby :
module Colors
BLUE = "\033[94m"
RED = "\033[31m"
STOP = "\033[0m"
end
def heapsort(rawNumbers)
numbers = rawNumbers.dup
def swap(numbers, from, to)
temp = numbers[from]
numbers[from] = numbers[to]
numbers[to] = temp
end
def heapify(numbers)
count = numbers.length()
lastParentNode = (count - 2) / 2
for start in lastParentNode.downto(0)
siftDown(numbers, start, count - 1)
start -= 1
end
if DEMO
puts "--- heapify ends ---"
end
end
def siftDown(numbers, start, rightBound)
cursor = start
printBinaryHeap(numbers, cursor, rightBound)
def calculateLhsChildIndex(cursor)
return cursor * 2 + 1
end
def calculateRhsChildIndex(cursor)
return cursor * 2 + 2
end
while calculateLhsChildIndex(cursor) <= rightBound
lhsChildIndex = calculateLhsChildIndex(cursor)
rhsChildIndex = calculateRhsChildIndex(cursor)
lhsNumber = numbers[lhsChildIndex]
biggerChildIndex = lhsChildIndex
if rhsChildIndex <= rightBound
rhsNumber = numbers[rhsChildIndex]
if lhsNumber < rhsNumber
biggerChildIndex = rhsChildIndex
end
end
if numbers[cursor] < numbers[biggerChildIndex]
swap(numbers, cursor, biggerChildIndex)
cursor = biggerChildIndex
else
break
end
printBinaryHeap(numbers, cursor, rightBound)
end
printBinaryHeap(numbers, cursor, rightBound)
end
def printBinaryHeap(numbers, nodeIndex = -1, rightBound = -1)
if DEMO == false
return
end
perLineWidth = (numbers.length() * 4).to_i
linesCount = Math.log2(numbers.length()).ceil()
xPrinterCount = 1
cursor = 0
spacing = 3
for y in (0..linesCount)
line = perLineWidth.times.map { " " }
spacing = spacing == 3 ? 4 : 3
printIndex = (perLineWidth / 2) - (spacing * xPrinterCount) / 2
for x in (0..xPrinterCount - 1)
if cursor >= numbers.length
break
end
if nodeIndex != -1 && cursor == nodeIndex
line[printIndex] = "%s%s%s" % [Colors::RED, numbers[cursor].to_s, Colors::STOP]
elsif rightBound != -1 && cursor > rightBound
line[printIndex] = "%s%s%s" % [Colors::BLUE, numbers[cursor].to_s, Colors::STOP]
else
line[printIndex] = numbers[cursor].to_s
end
cursor += 1
printIndex += spacing
end
print line.join()
xPrinterCount *= 2
print "\n"
end
end
heapify(numbers)
rightBound = numbers.length() - 1
while rightBound > 0
swap(numbers, 0, rightBound)
rightBound -= 1
siftDown(numbers, 0, rightBound)
end
return numbers
end
numbersCount = 14
maximalNumber = 10
numbers = numbersCount.times.map { Random.rand(maximalNumber) }
print numbers
print "\n---\n"
start = Time.now
sortedNumbers = heapsort(numbers)
finish = Time.now
heapSortTime = start - finish
start = Time.now
referenceSortedNumbers = numbers.sort()
finish = Time.now
referenceSortTime = start - finish
print "Reference sort: "
print referenceSortedNumbers
print "\n"
print "Reference sort time: %f\n" % referenceSortTime
print "Heap sort: "
print sortedNumbers
print "\n"
if DEMO == false
print "Heap sort time: %f\n" % heapSortTime
else
print "Disable DEMO for performance measure\n"
end
if sortedNumbers != referenceSortedNumbers
puts "Validation failed"
exit 1
else
puts "Validation success"
exit 0
end
Cet algorithme n’est pas facile à comprendre sans visualisation, donc la première chose que je recommande est d’écrire une fonction qui imprimera la vue actuelle de l’arbre binaire.
Liens
https://gitlab.com/demensdeum/algorithms/-/blob/master/sortAlgorithms/heapsort/heapsort.rb
Sources
http://rosettacode.org/wiki/Sorting_algorithms/Heapsort
https://www.youtube.com/watch?v=LbB357_RwlY
https://habr.com/ru/company/ otus/blog/460087/
https://ru.wikipedia.org/wiki/Pyramid_sort
https://neerc.ifmo.ru/wiki /index.php?title=Heap_sort
https://wiki5.ru/wiki/Heapsort
https://ru.wikipedia.org/wiki/Tree (structure des données)
https://ru.wikipedia.org/wiki/Heap (structure des données)
https://www.youtube.com/watch?v=2DmK_H7IdTo
https://www.youtube.com/watch?v=kU4KBD4NFtw
https://www.youtube.com/watch?v=DU1uG5310x0
https://www.youtube.com/watch?v =BzQGPA_v-vc
https://www.geeksforgeeks.org/ représentation-tableau-de-tas-binaire/
https://habr.com/ru/post/112222/
https://www.cs.usfca. edu/~galles/visualization/BST.html
https://www.youtube.com/watch?v=EQzqHWtsKq4
https://ru.wikibrief.org/wiki/Heapsort
https://www.youtube.com/watch?v=GUUpmrTnNbw
Tri rapide
Quicksort est un algorithme de tri diviser pour régner. De manière récursive, pièce par pièce, nous analysons le tableau de nombres, en plaçant les nombres dans un ordre de plus en plus grand à partir de l’élément de référence sélectionné, et insérons l’élément de référence lui-même dans la coupure entre eux. Après plusieurs itérations récursives, vous vous retrouverez avec une liste triée. Complexité temporelle O(n2).
Schéma :
- Nous commençons par obtenir une liste d’éléments de l’extérieur, les limites de tri. Dans un premier temps, les limites de tri s’étendront du début à la fin.
- Vérifiez que les limites de début et de fin ne se croisent pas ; si cela se produit, il est temps de terminer
- Sélectionnez un élément dans la liste et appelez-le pivot
- Déplacez-le vers la droite jusqu’à la fin du dernier index afin qu’il ne gêne pas
- Créez un compteur de *nombres plus petits* toujours égaux à zéro
- Parcourez la liste de gauche à droite, jusqu’au dernier index inclus où se trouve l’élément de référence
- Nous comparons chaque élément avec celui de référence
- S’il est inférieur à celui de référence, alors nous l’échangeons en fonction de l’index du compteur des nombres plus petits. Incrémentez le compteur des nombres plus petits.
- Lorsque la boucle atteint l’élément de support, nous nous arrêtons et échangeons l’élément de support avec l’élément en fonction du compteur de nombres plus petits.
- Nous exécutons l’algorithme séparément pour la plus petite partie gauche de la liste et séparément pour la plus grande partie droite de la liste.
- Par conséquent, toutes les itérations récursives commenceront à s’arrêter en raison de l’enregistrement au point 2
- Obtenir une liste triée
Quicksort a été inventé par le scientifique Charles Anthony Richard Hoare de l’Université d’État de Moscou. Ayant appris le russe, il a étudié la traduction informatique ainsi que la théorie des probabilités à l’école Kolmogorov. En 1960, en raison de la crise politique, il quitte l’Union soviétique.
Exemple d’implémentation dans Rust :
use rand::Rng;
fn swap(numbers: &mut [i64], from: usize, to: usize) {
let temp = numbers[from];
numbers[from] = numbers[to];
numbers[to] = temp;
}
fn quicksort(numbers: &mut [i64], left: usize, right: usize) {
if left >= right {
return
}
let length = right - left;
if length <= 1 {
return
}
let pivot_index = left + (length / 2);
let pivot = numbers[pivot_index];
let last_index = right - 1;
swap(numbers, pivot_index, last_index);
let mut less_insert_index = left;
for i in left..last_index {
if numbers[i] < pivot {
swap(numbers, i, less_insert_index);
less_insert_index += 1;
}
}
swap(numbers, last_index, less_insert_index);
quicksort(numbers, left, less_insert_index);
quicksort(numbers, less_insert_index + 1, right);
}
fn main() {
let mut numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut reference_numbers = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
let mut rng = rand::thread_rng();
for i in 0..numbers.len() {
numbers[i] = rng.gen_range(-10..10);
reference_numbers[i] = numbers[i];
}
reference_numbers.sort();
println!("Numbers {:?}", numbers);
let length = numbers.len();
quicksort(&mut numbers, 0, length);
println!("Numbers {:?}", numbers);
println!("Reference numbers {:?}", reference_numbers);
if numbers != reference_numbers {
println!("Validation failed");
std::process::exit(1);
}
else {
println!("Validation success!");
std::process::exit(0);
}
}
Si rien n’est clair, je vous suggère de regarder la vidéo de Rob Edwards de l’Université de San Diego https://www.youtube.com/watch?v=ZHVk2blR45Q il montre très simplement, étape par étape, l’essence et la mise en œuvre de l’algorithme.
Liens
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/quickSort
Sources
https://www.youtube.com/watch?v =4s-aG6yGGLU
https://www.youtube.com/watch?v=ywWBy6J5gz8
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://ru.wikipedia.org/wiki/Быстрая_сортировка
https://www.youtube.com/watch?v=Hoixgm4-P4M
https://www.youtube.com/watch?v=XE4VP_8Y0BU
https://www.youtube.com/watch?v=MZaf_9IZCrc
https://www.youtube.com/watch?v=ZHVk2blR45Q
http://rosettacode.org/wiki/Sorting_algorithms/Quicksort
https://www.youtube.com/watch?v=4s-aG6yGGLU
https://www.youtube.com/watch?v=dQw4w9WgXcQ
https://www.youtube.com/watch?v=maibrCbZWKw
https://www.geeksforgeeks.org/quick-sort/
https://www.youtube.com/watch?v=uXBnyYuwPe8
Tri par insertion binaire
Le tri par insertion binaire est une variante du tri par insertion dans laquelle la position d’insertion est déterminée à l’aide d’une recherche binaire. La complexité temporelle de l’algorithme est O(n2)
L’algorithme fonctionne comme ceci :
- Une boucle commence de zéro jusqu’à la fin de la liste
- Dans la boucle, un nombre est sélectionné pour le tri, le nombre est stocké dans une variable distincte
- La recherche binaire recherche l’index pour insérer ce numéro par rapport aux chiffres de gauche
- Une fois l’index trouvé, les nombres de gauche sont décalés d’une position vers la droite, en commençant à l’index d’insertion. Au cours du processus, le numéro à trier sera effacé.
- Le numéro précédemment enregistré est inséré à l’index d’insertion
- A la fin de la boucle, toute la liste sera triée
Lors d’une recherche binaire, il est possible que le numéro ne soit pas trouvé et que l’index ne soit pas renvoyé. En raison de la particularité de la recherche binaire, le nombre le plus proche de celui recherché sera trouvé, puis pour renvoyer l’index il faudra le comparer avec celui recherché, si celui recherché est inférieur, alors celui recherché doit être à l’index à gauche, et s’il est supérieur ou égal, alors à droite.
Allez code :
import (
"fmt"
"math/rand"
"time"
)
const numbersCount = 20
const maximalNumber = 100
func binarySearch(numbers []int, item int, low int, high int) int {
for high > low {
center := (low + high) / 2
if numbers[center] < item { low = center + 1 } else if numbers[center] > item {
high = center - 1
} else {
return center
}
}
if numbers[low] < item {
return low + 1
} else {
return low
}
}
func main() {
rand.Seed(time.Now().Unix())
var numbers [numbersCount]int
for i := 0; i < numbersCount; i++ {
numbers[i] = rand.Intn(maximalNumber)
}
fmt.Println(numbers)
for i := 1; i < len(numbers); i++ { searchAreaLastIndex := i - 1 insertNumber := numbers[i] insertIndex := binarySearch(numbers[:], insertNumber, 0, searchAreaLastIndex) for x := searchAreaLastIndex; x >= insertIndex; x-- {
numbers[x+1] = numbers[x]
}
numbers[insertIndex] = insertNumber
}
fmt.Println(numbers)
}
Liens
Sources
https://www.geeksforgeeks.org/binary-insertion- trier/
https://www.youtube.com/watch?v=-OVB5pOZJug
Tri des coquilles
Shell Sort – une variante du tri par insertion avec peignage préliminaire d’un tableau de nombres.
Nous devons nous rappeler comment fonctionne le tri par insertion :
1. Une boucle commence de zéro jusqu’à la fin de la boucle, le tableau est donc divisé en deux parties
2. Pour la partie gauche, une deuxième boucle est lancée, comparant les éléments de droite à gauche, le plus petit élément de droite est déposé jusqu’à ce qu’un plus petit élément de gauche soit trouvé
3. A la fin des deux boucles, on obtient une liste triée
Il était une fois l’informaticien Donald Schell qui se demandait comment améliorer l’algorithme de tri par insertion. Il a également eu l’idée de parcourir d’abord le tableau en deux cycles, mais à une certaine distance, en réduisant progressivement le « peigne » jusqu’à ce qu’il se transforme en un algorithme de tri par insertion régulier. Tout est vraiment si simple, pas d’embûches, aux deux cycles ci-dessus on en ajoute un autre, dans lequel on réduit progressivement la taille du « peigne ». La seule chose que vous devez faire est de vérifier la distance lors de la comparaison afin qu’elle ne dépasse pas le tableau.
Un sujet vraiment intéressant est le choix de la séquence permettant de modifier la longueur de comparaison à chaque itération de la première boucle. C’est intéressant car les performances de l’algorithme en dépendent.
Le tableau des options connues et de la complexité temporelle peut être trouvé ici : https : //fr .wikipedia.org/wiki/Shellsort#Gap_sequences
Différentes personnes ont participé au calcul de la distance idéale ; apparemment, ce sujet les intéressait beaucoup. Ne pourraient-ils pas simplement exécuter Ruby et appeler l’algorithme sort() le plus rapide ?
En général, ces personnes étranges ont écrit des dissertations sur le thème du calcul de la distance/écart du « peigne » pour l’algorithme Shell. J’ai simplement utilisé les résultats de leurs travaux et vérifié 5 types de séquences, Hibbard, Knuth-Pratt, Chiura, Sedgwick.
import time
import random
from functools import reduce
import math
DEMO_MODE = False
if input("Demo Mode Y/N? ").upper() == "Y":
DEMO_MODE = True
class Colors:
BLUE = '\033[94m'
RED = '\033[31m'
END = '\033[0m'
def swap(list, lhs, rhs):
list[lhs], list[rhs] = list[rhs], list[lhs]
return list
def colorPrintoutStep(numbers: List[int], lhs: int, rhs: int):
for index, number in enumerate(numbers):
if index == lhs:
print(f"{Colors.BLUE}", end = "")
elif index == rhs:
print(f"{Colors.RED}", end = "")
print(f"{number},", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
if index == lhs or index == rhs:
print(f"{Colors.END}", end = "")
print("\n")
input(">")
def ShellSortLoop(numbers: List[int], distanceSequence: List[int]):
distanceSequenceIterator = reversed(distanceSequence)
while distance:= next(distanceSequenceIterator, None):
for sortArea in range(0, len(numbers)):
for rhs in reversed(range(distance, sortArea + 1)):
lhs = rhs - distance
if DEMO_MODE:
print(f"Distance: {distance}")
colorPrintoutStep(numbers, lhs, rhs)
if numbers[lhs] > numbers[rhs]:
swap(numbers, lhs, rhs)
else:
break
def ShellSort(numbers: List[int]):
global ShellSequence
ShellSortLoop(numbers, ShellSequence)
def HibbardSort(numbers: List[int]):
global HibbardSequence
ShellSortLoop(numbers, HibbardSequence)
def ShellPlusKnuttPrattSort(numbers: List[int]):
global KnuttPrattSequence
ShellSortLoop(numbers, KnuttPrattSequence)
def ShellPlusCiuraSort(numbers: List[int]):
global CiuraSequence
ShellSortLoop(numbers, CiuraSequence)
def ShellPlusSedgewickSort(numbers: List[int]):
global SedgewickSequence
ShellSortLoop(numbers, SedgewickSequence)
def insertionSort(numbers: List[int]):
global insertionSortDistanceSequence
ShellSortLoop(numbers, insertionSortDistanceSequence)
def defaultSort(numbers: List[int]):
numbers.sort()
def measureExecution(inputNumbers: List[int], algorithmName: str, algorithm):
if DEMO_MODE:
print(f"{algorithmName} started")
numbers = inputNumbers.copy()
startTime = time.perf_counter()
algorithm(numbers)
endTime = time.perf_counter()
print(f"{algorithmName} performance: {endTime - startTime}")
def sortedNumbersAsString(inputNumbers: List[int], algorithm) -> str:
numbers = inputNumbers.copy()
algorithm(numbers)
return str(numbers)
if DEMO_MODE:
maximalNumber = 10
numbersCount = 10
else:
maximalNumber = 10
numbersCount = random.randint(10000, 20000)
randomNumbers = [random.randrange(1, maximalNumber) for i in range(numbersCount)]
ShellSequenceGenerator = lambda n: reduce(lambda x, _: x + [int(x[-1]/2)], range(int(math.log(numbersCount, 2))), [int(numbersCount / 2)])
ShellSequence = ShellSequenceGenerator(randomNumbers)
ShellSequence.reverse()
ShellSequence.pop()
HibbardSequence = [
0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095,
8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575,
2097151, 4194303, 8388607, 16777215, 33554431, 67108863, 134217727,
268435455, 536870911, 1073741823, 2147483647, 4294967295, 8589934591
]
KnuttPrattSequence = [
1, 4, 13, 40, 121, 364, 1093, 3280, 9841, 29524, 88573, 265720,
797161, 2391484, 7174453, 21523360, 64570081, 193710244, 581130733,
1743392200, 5230176601, 15690529804, 47071589413
]
CiuraSequence = [
1, 4, 10, 23, 57, 132, 301, 701, 1750, 4376,
10941, 27353, 68383, 170958, 427396, 1068491,
2671228, 6678071, 16695178, 41737946, 104344866,
260862166, 652155416, 1630388541
]
SedgewickSequence = [
1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905,
8929, 16001, 36289, 64769, 146305, 260609, 587521,
1045505, 2354689, 4188161, 9427969, 16764929, 37730305,
67084289, 150958081, 268386305, 603906049, 1073643521,
2415771649, 4294770689, 9663381505, 17179475969
]
insertionSortDistanceSequence = [1]
algorithms = {
"Default Python Sort": defaultSort,
"Shell Sort": ShellSort,
"Shell + Hibbard" : HibbardSort,
"Shell + Prat, Knutt": ShellPlusKnuttPrattSort,
"Shell + Ciura Sort": ShellPlusCiuraSort,
"Shell + Sedgewick Sort": ShellPlusSedgewickSort,
"Insertion Sort": insertionSort
}
for name, algorithm in algorithms.items():
measureExecution(randomNumbers, name, algorithm)
reference = sortedNumbersAsString(randomNumbers, defaultSort)
for name, algorithm in algorithms.items():
if sortedNumbersAsString(randomNumbers, algorithm) != reference:
print("Sorting validation failed")
exit(1)
print("Sorting validation success")
exit(0)
Dans mon implémentation, pour un ensemble aléatoire de nombres, les écarts les plus rapides sont Sedgwick et Hibbard.
monpy
Je voudrais également mentionner l’analyseur de typage statique pour Python 3 – mypy. Aide à faire face aux problèmes inhérents aux langages à typage dynamique, à savoir qu’il élimine la possibilité de coller quelque chose là où ce n’est pas nécessaire.
Comme le disent les programmeurs expérimentés, “la saisie statique n’est pas nécessaire lorsque vous avez une équipe de professionnels”, un jour nous deviendrons tous des professionnels, nous écrirons du code en pleine unité et compréhension avec les machines, mais pour l’instant vous pouvez utiliser des utilitaires similaires. et les langages typés statiquement.
Liens
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/shellSort
http://mypy-lang.org/
Sources
https://dl.acm.org/doi/10.1145/368370.368387
https://en.wikipedia.org/wiki/Shellsort
http://rosettacode.org/wiki/Sorting_algorithms/Shell_sort
https://ru.wikipedia.org/wiki/Сортировка_Шелла
https://neerc.ifmo.ru/wiki/index.php?title=Сортировка_Шелла
https://twitter.com/gvanrossum/status/700741601966985216
Tri à double sélection
Tri par sélection double : un sous-type de tri par sélection, il semble qu’il devrait être deux fois plus rapide. L’algorithme Vanilla effectue une double boucle dans la liste des nombres, trouve le nombre minimum et échange les places avec le numéro actuel pointé par la boucle au niveau supérieur. Le tri par double sélection recherche les nombres minimum et maximum, puis remplace les deux chiffres pointés par la boucle au niveau supérieur à – deux chiffres à gauche et à droite. Toute cette orgie se termine lorsque les curseurs des nombres à remplacer se trouvent au milieu de la liste, et par conséquent, des nombres triés sont obtenus à gauche et à droite du centre visuel.
La complexité temporelle de l’algorithme est similaire à celle du tri par sélection – O(n2), mais soi-disant il y a une accélération de 30 %.
État limite
Déjà à ce stade, vous pouvez imaginer le moment d’une collision, par exemple, lorsque le numéro du curseur gauche (le nombre minimum) pointe vers le nombre maximum dans la liste, alors le nombre minimum est réorganisé, le réarrangement du nombre maximum tombe immédiatement en panne. Par conséquent, toutes les implémentations de l’algorithme contiennent la vérification de tels cas et le remplacement des index par des index corrects. Dans mon implémentation, une seule vérification suffisait :
maximalNumberIndex = minimalNumberIndex;
}Реализация на Cito
Cito – язык либ, язык транслятор. На нем можно писать для C, C++, C#, Java, JavaScript, Python, Swift, TypeScript, OpenCL C, при этом совершенно ничего не зная про эти языки. Исходный код на языке Cito транслируется в исходный код на поддерживаемых языках, далее можно использовать как библиотеку, либо напрямую, исправив сгенеренный код руками. Эдакий Write once – translate to anything.
Double Selection Sort на cito:
{
public static int[] sort(int[]# numbers, int length)
{
int[]# sortedNumbers = new int[length];
for (int i = 0; i < length; i++) {
sortedNumbers[i] = numbers[i];
}
for (int leftCursor = 0; leftCursor < length / 2; leftCursor++) {
int minimalNumberIndex = leftCursor;
int minimalNumber = sortedNumbers[leftCursor];
int rightCursor = length - (leftCursor + 1);
int maximalNumberIndex = rightCursor;
int maximalNumber = sortedNumbers[maximalNumberIndex];
for (int cursor = leftCursor; cursor <= rightCursor; cursor++) { int cursorNumber = sortedNumbers[cursor]; if (minimalNumber > cursorNumber) {
minimalNumber = cursorNumber;
minimalNumberIndex = cursor;
}
if (maximalNumber < cursorNumber) {
maximalNumber = cursorNumber;
maximalNumberIndex = cursor;
}
}
if (leftCursor == maximalNumberIndex) {
maximalNumberIndex = minimalNumberIndex;
}
int fromNumber = sortedNumbers[leftCursor];
int toNumber = sortedNumbers[minimalNumberIndex];
sortedNumbers[minimalNumberIndex] = fromNumber;
sortedNumbers[leftCursor] = toNumber;
fromNumber = sortedNumbers[rightCursor];
toNumber = sortedNumbers[maximalNumberIndex];
sortedNumbers[maximalNumberIndex] = fromNumber;
sortedNumbers[rightCursor] = toNumber;
}
return sortedNumbers;
}
}
Liens
https://gitlab.com/demensdeum /algorithms/-/tree/master/sortAlgorithms/doubleSelectionSort
https://github.com/pfusik/cito
Sources
https://www.researchgate.net/publication/330084245_Improved_Double_Selection_Sort_using_Algorithm
http://algolab.valemak.com/selection-double
https://www.geeksforgeeks.org/sorting-algorithm-slightly-improves-selection-sort/