Tutorials

Selection Sort

Selection Sort – selection sorting algorithm. Selection of what? The minimum number!!!
The time complexity of the algorithm is O(n²)

The algorithm works as follows:

We go through the array in a loop from left to right, remember the current starting index and the number by index, we will call the number A
Inside the loop, we start another one to go from left to right in search of something smaller than A
When we find the smaller one, we remember the index, now the smaller one becomes the number A
When the inner loop ends, swap the number at the starting index with the number A
After the full pass of the upper loop, we get a sorted array

Example of algorithm execution:

(29, 49, 66, 35, 7, 12, 80)
29 > 7
(7, 49, 66, 35, 29, 12, 80)
Round 1 ENDED
Round 2
(7, 49, 66, 35, 29, 12, 80)
49 > 35
35 > 29
29 > 12
(7, 12, 66, 35, 29, 49, 80)
Round 2 ENDED
Round 3
(7, 12, 66, 35, 29, 49, 80)
66 > 35
35 > 29
(7, 12, 29, 35, 66, 49, 80)
Round 3 ENDED
Round 4
(7, 12, 29, 35, 66, 49, 80)
(7, 12, 29, 35, 66, 49, 80)
Round 4 ENDED
Round 5
(7, 12, 29, 35, 66, 49, 80)
66 > 49
(7, 12, 29, 35, 49, 66, 80)
Round 5 ENDED
Round 6
(7, 12, 29, 35, 49, 66, 80)
(7, 12, 29, 35, 49, 66, 80)
Round 6 ENDED
Sorted: (7, 12, 29, 35, 49, 66, 80)

Having failed to find an Objective-C implementation on Rosetta Code, I wrote it myself:

#include <Foundation/Foundation.h>

@implementation SelectionSort
- (void)performSort:(NSMutableArray *)numbers
{
   NSLog(@"%@", numbers);   
   for (int startIndex = 0; startIndex < numbers.count-1; startIndex++) {
      int minimalNumberIndex = startIndex;
      for (int i = startIndex + 1; i < numbers.count; i++) {
         id lhs = [numbers objectAtIndex: minimalNumberIndex];
         id rhs = [numbers objectAtIndex: i];
         if ([lhs isGreaterThan: rhs]) {
            minimalNumberIndex = i;
         }
      }
      id temporary = [numbers objectAtIndex: minimalNumberIndex];
      [numbers setObject: [numbers objectAtIndex: startIndex] 
               atIndexedSubscript: minimalNumberIndex];
      [numbers setObject: temporary
               atIndexedSubscript: startIndex];
   }
   NSLog(@"%@", numbers);
}

@end

Собрать и запустить можно либо на MacOS/Xcode, либо на любой операционной системе поддерживающей GNUstep, например у меня собирается Clang на Arch Linux.
Скрипт сборки:

        main.m \
        -lobjc \
        `gnustep-config --objc-flags` \
        `gnustep-config --objc-libs` \
        -I /usr/include/GNUstepBase \
        -I /usr/lib/gcc/x86_64-pc-linux-gnu/12.1.0/include/ \
        -lgnustep-base \
        -o SelectionSort \

Links

https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/selectionSort

Sources

https://rosettacode.org/wiki/Sorting_algorithms/Selection_sort
https://ru.wikipedia.org/wiki/Сортировка_выбором
https://en.wikipedia.org/wiki/Selection_sort
https://www.youtube.com/watch?v=LJ7GYbX7qpM

Counting Sort

Counting sort – the algorithm of sorting by counting. What do you mean? Yes! Just like that!

The algorithm involves at least two arrays, the first is a list of integers to be sorted, the second is an array of size = (maximum number – minimum number) + 1, initially containing only zeros. Then the numbers from the first array are sorted, the index in the second array is obtained by the number element, which is incremented by one. After going through the entire list, we get a completely filled second array with the number of repetitions of numbers from the first. The algorithm has a serious overhead – the second array also contains zeros for numbers that are not in the first list, the so-called memory overhead.

After receiving the second array, we iterate over it and write the sorted version of the number by index, decrementing the counter to zero. The initially zero counter is ignored.

An example of unoptimized operation of the counting sort algorithm:

Input array 1,9,1,4,6,4,4
Then the array to count will be 0,1,2,3,4,5,6,7,8,9 (minimum number 0, maximum 9)
With final counters 0,2,0,0,3,0,1,0,0,1
Total sorted array 1,1,4,4,4,6,9

Algorithm code in Python 3:


numbers = [42, 89, 69, 777, 22, 35, 42, 69, 42, 90, 777]

minimal = min(numbers)
maximal = max(numbers)
countListRange = maximal - minimal
countListRange += 1
countList = [0] * countListRange

print(numbers)
print(f"Minimal number: {minimal}")
print(f"Maximal number: {maximal}")
print(f"Count list size: {countListRange}")

for number in numbers:
    index = number - minimal
    countList[index] += 1

replacingIndex = 0
for index, count in enumerate(countList):
    for i in range(count):
        outputNumber = minimal + index
        numbers[replacingIndex] = outputNumber
        replacingIndex += 1

print(numbers)

Из-за использования двух массивов, временная сложность алгоритма O(n + k)

Ссылки

https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/countingSort

Источники

https://www.youtube.com/watch?v=6dk_csyWif0
https://www.youtube.com/watch?v=OKd534EWcdk
https://en.wikipedia.org/wiki/Counting_sort
https://rosettacode.org/wiki/Sorting_algorithms/Counting_sort
https://pro-prof.com/forums/topic/%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC-%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B8-%D0%BF%D0%BE%D0%B4%D1%81%D1%87%D0%B5%D1%82%D0%BE%D0%BC

Bogosort

Pseudo-sort or swamp sort, one of the most useless sorting algorithms.

It works like this:
1. An array of numbers is fed to the input
2. An array of numbers is shuffled randomly
3. Check if the array is sorted
4. If not sorted, the array is shuffled again
5. This whole process is repeated until the array is sorted randomly.

As you can see, the performance of this algorithm is terrible, smart people think that even O(n * n!), i.e. there is a chance to get stuck throwing dice for the glory of the god of chaos for many years, the array will still not be sorted, or maybe it will be sorted?

Implementation

To implement it in TypeScript, I needed to implement the following functions:
1. Shuffling an array of objects
2. Comparison of arrays
3. Generate a random number in the range from zero to a number (sic!)
4. Print progress, because it seems like sorting is going on forever

Below is the implementation code in TypeScript:

const randomInteger = (maximal: number) => Math.floor(Math.random() * maximal);
const isEqual = (lhs: any[], rhs: any[]) => lhs.every((val, index) => val === rhs[index]);
const shuffle = (array: any[]) => {
    for (var i = 0; i < array.length; i++) { var destination = randomInteger(array.length-1); var temp = array[i]; array[i] = array[destination]; array[destination] = temp; } } let numbers: number[] = Array.from({length: 10}, ()=>randomInteger(10));
const originalNumbers = [...numbers];
const sortedNumbers = [...numbers].sort();

let numberOfRuns = 1;

do {
    if (numberOfRuns % 1000 == 0) {
        printoutProcess(originalNumbers, numbers, numberOfRuns);
    }
    shuffle(numbers);
    numberOfRuns++;
} while (isEqual(numbers, sortedNumbers) == false)

console.log(`Success!`);
console.log(`Run number: ${numberOfRuns}`)
console.log(`Original numbers: ${originalNumbers}`);
console.log(`Current numbers: ${originalNumbers}`);
console.log(`Sorted numbers: ${sortedNumbers}`);

Для отладки можно использовать VSCode и плагин TypeScript Debugger от kakumei.

Как долго

Вывод работы алгоритма:

src/bogosort.ts:1
Still trying to sort: 5,4,8,7,5,0,2,9,7,2, current shuffle 8,7,0,2,4,7,2,5,9,5, try number: 145000
src/bogosort.ts:2
Still trying to sort: 5,4,8,7,5,0,2,9,7,2, current shuffle 7,5,2,4,9,8,0,5,2,7, try number: 146000
src/bogosort.ts:2
Still trying to sort: 5,4,8,7,5,0,2,9,7,2, current shuffle 0,2,7,4,9,5,7,5,8,2, try number: 147000
src/bogosort.ts:2
Still trying to sort: 5,4,8,7,5,0,2,9,7,2, current shuffle 5,9,7,8,5,4,2,7,0,2, try number: 148000
src/bogosort.ts:2
Success!
src/bogosort.ts:24
Run number: 148798
src/bogosort.ts:25
Original numbers: 5,4,8,7,5,0,2,9,7,2
src/bogosort.ts:26
Current numbers: 5,4,8,7,5,0,2,9,7,2
src/bogosort.ts:27
Sorted numbers: 0,2,2,4,5,5,7,7,8,9

Для массива из 10 чисел Богосорт перемешивал исходный массив 148798 раз, многовато да?
Алгоритм можно использовать как учебный, для понимания возможностей языка с которым предстоит работать на рынке. Лично я был удивлен узнав что в ванильных JS и TS до сих пор нет своего алгоритма перемешивания массивов, генерации целого числа в диапазоне, доступа к хэшам объектов для быстрого сравнения.

Ссылки

https://gitlab.com/demensdeum/algorithms/-/tree/master/sortAlgorithms/bogosort
https://www.typescriptlang.org/
https://marketplace.visualstudio.com/items?itemName=kakumei.ts-debug

Источники

https://www.youtube.com/watch?v=r2N3scbd_jg
https://en.wikipedia.org/wiki/Bogosort

GoF Patterns

List of Gang of Four patterns – the very patterns that can get you flunked at an interview.

Generative Patterns

Structural patterns

Patterns of behavior

Pattern Interpreter

What’s included

The Interpreter pattern is a Behavioral design pattern. This pattern allows you to implement your own programming language by working with an AST tree, the nodes of which are terminal and non-terminal expressions that implement the Interpret method, which provides the functionality of the language.

Terminal expression – for example, the string constant – “Hello World”
A non-terminal expression – for example Print(“Hello World”) – contains Print and the argument from the Terminal expression “Hello World”

What is the difference? The difference is that interpretation ends on terminal expressions, and for non-terminal expressions it continues in depth along all incoming nodes/arguments. If the AST tree consisted only of non-terminal expressions, then the application execution would never be completed, since some finiteness of any process is required, and this finiteness is represented by terminal expressions, they usually contain data, such as strings.

An example of an AST tree is below:

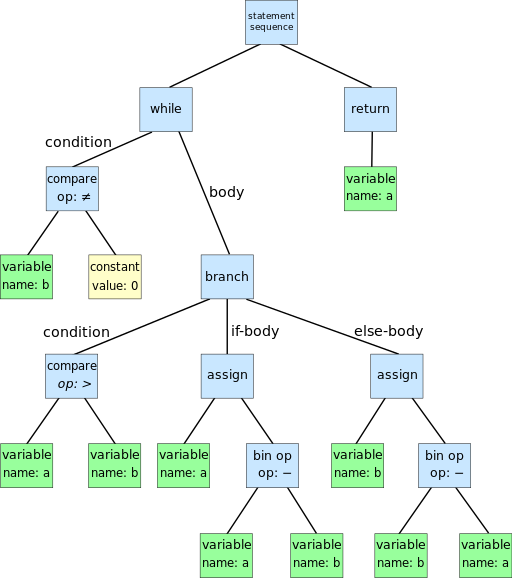
Dcoetzee, CC0, via Wikimedia Commons

As you can see, terminal expressions are constant and variable, non-terminal expressions are the rest.

What is not included

The implementation of the Interpreter does not include parsing the language string input into an AST tree. It is enough to implement classes of terminal, non-terminal expressions, Interpret methods with the Context argument at the input, format the AST tree from expressions, and run the Interpret method at the root expression. The context can be used to store the application state during execution.

Implementation

The pattern involves:

Client – returns the AST tree and runs Interpret(context) for the root node (Client)
Context – contains the state of the application, passed to expressions during interpretation (Context)
Abstract expression – an abstract class containing the Interpret(context) (Expression) method
A terminal expression is a final expression, a descendant of an abstract expression (TerminalExpression)
A non-terminal expression is not a final expression, it contains pointers to nodes deep in the AST tree, subordinate nodes usually affect the result of interpreting the non-terminal expression (NonTerminalExpression)

C# Client Example

        static void Main(string[] args)
        {
            var context = new Context();
            var initialProgram = new PerformExpression(
                new IExpression[] {
                    new SetExpression("alpha", "1"),
                    new GetExpression("alpha"),
                    new PrintExpression(
                        new IExpression[] {
                            new ConstantExpression("Hello Interpreter Pattern")
                        }
                    )
                }
            );
            System.Console.WriteLine(initialProgram.interpret(context));
        }
}

Abstract Expression Example in C#

{
    String interpret(Context context);
}

Example of Terminal Expression in C# (String Constant)

{
    private String constant;

    public ConstantExpression(String constant) {
        this.constant = constant;
    }

    override public String interpret(Context context) {
        return constant;
    }
}

Example of Non-Terminal Expression in C# (Start and concatenate results of subordinate nodes, using the separator “;”

{
    public PerformExpression(IExpression[] leafs) : base(leafs) {
        this.leafs = leafs;
    }
    
    override public String interpret(Context context) {
        var output = "";
        foreach (var leaf in leafs) {
            output += leaf.interpret(context) + ";";
        }
        return output;
    }
}

Can you do it functionally?

As we know, all Turing-complete languages are equivalent. Is it possible to transfer the Object-Oriented pattern to the Functional programming language?

For the experiment, we can take the FP language for the web called Elm. Elm does not have classes, but it does have Records and Types, so the following records and types are involved in the implementation:

Expression – an enumeration of all possible expressions of the language (Expression)
Subordinate expression – an expression that is subordinate to a Nonterminal expression (ExpressionLeaf)
Context – a record that stores the state of the application (Context)
Functions implementing Interpret(context) methods – all necessary functions implementing the functionality of Terminal, Non-terminal expressions
Auxiliary records of the Interpreter state – necessary for the correct operation of the Interpreter, store the state of the Interpreter, context

An example of a function implementing interpretation for the entire set of possible expressions in Elm:

  case input.expression of
    Constant text ->
      { 
        output = text, 
        context = input.context 
      }
    Perform leafs ->
      let inputs = List.map (\leaf -> { expressionLeaf = leaf, context = input.context } ) leafs in
        let startLeaf = { expressionLeaf = (Node (Constant "")), context = { variables = Dict.empty } } in
          let outputExpressionInput = List.foldl mergeContextsAndRunLeafs startLeaf inputs in
            {
              output = (runExpressionLeaf outputExpressionInput).output,
              context = input.context
            }
    Print printExpression ->
      run 
      { 
        expression = printExpression, 
        context = input.context 
      }
    Set key value ->
      let variables = Dict.insert key value input.context.variables in
      {
        output = "OK",
        context = { variables = variables }
      }
    Get key ->
      {
        output = Maybe.withDefault ("No value for key: " ++ key) (Dict.get key input.context.variables),
        context = input.context
      }

And parse?

Parsing source code into an AST tree is not part of the Interpreter pattern, there are several approaches to parsing source code, but we’ll talk about that some other time.
In the implementation of the Interpreter for Elm, I wrote the simplest parser in the AST tree, consisting of two functions – parsing the node, parsing the subordinate nodes.

parseLeafs state =
    let tokensQueue = state.tokensQueue in
        let popped = pop state.tokensQueue in
            let tokensQueueTail = tail state.tokensQueue in
                if popped == "Nothing" then
                    state
                else if popped == "Perform(" then
                    {
                        tokensQueue = tokensQueue,
                        result = (state.result ++ [Node (parse tokensQueue)])
                    }
                else if popped == ")" then
                    parseLeafs {
                        tokensQueue = tokensQueueTail,
                        result = state.result
                    }
                else if popped == "Set" then
                    let key = pop tokensQueueTail in
                        let value = pop (tail tokensQueueTail) in
                            parseLeafs {
                                tokensQueue = tail (tail tokensQueueTail),
                                result = (state.result ++ [Node (Set key value)])
                            }
                else if popped == "Get" then
                    let key = pop tokensQueueTail in
                        parseLeafs {
                            tokensQueue = tail tokensQueueTail,
                            result = (state.result ++ [Node (Get key)])
                        }
                else 
                    parseLeafs {
                        tokensQueue = tokensQueueTail,
                        result = (state.result ++ [Node (Constant popped)])
                    }

parse tokensQueue =
    let popped = pop tokensQueue in
        let tokensQueueTail = tail tokensQueue in
            if popped == "Perform(" then
                Perform (
                    parseLeafs {
                        tokensQueue = tokensQueueTail, 
                        result = []
                    }
                ).result
            else if popped == "Set" then
                let key = pop tokensQueueTail in
                    let value = pop (tail tokensQueueTail) in
                        Set key value
            else if popped == "Print" then
                Print (parse tokensQueueTail)
            else
                Constant popped

Links

https://gitlab.com/demensdeum /patterns/-/tree/master/interpreter/elm
https://gitlab.com/demensdeum/patterns/-/tree/master/interpreter/csharp

Sources

https://en.wikipedia.org/wiki/Interpreter_pattern
https://elm-lang.org/
https://docs.microsoft.com/en-us/dotnet/csharp/

RGB image to grayscale

In this note I will describe the algorithm for converting an RGB buffer to grayscale.
And this is done quite simply, each pixel of the buffer’s color channel is transformed according to a certain formula and the output is a gray image.
Average method:

red = average;
green = average;
blue = average;

Складываем 3 цветовых канала и делим на 3.

Однако существует еще один метод – метод средневзвешенный, он учитывает цветовосприятие человека:

red = luminance;
green = luminance;
blue = luminance;

Какой метод лучше использовать? Да какой вам больше подходит для конкретной задачи. Далее сравнение методов с помощью тестовой цветовой сетки:

Пример реализации на JavaScript + HTML 5

    image,
    canvas,
    weightedAverage
) {
    const context = canvas.getContext('2d');

    const imageWeight = image.width;
    const imageHeight = image.height;

    canvas.width = imageWeight;
    canvas.height = imageHeight;

    context.drawImage(image, 0, 0);

    let pixels = context
        .getImageData(
            0,
            0,
            imageWeight,
            imageHeight
        );

    for (let y = 0; y & lt; pixels.height; y++) {
        for (let x = 0; x & lt; pixels.width; x++) {
            const i = (y * 4) * pixels.width + x * 4;

            let red = pixels.data[i];
            let green = pixels.data[i + 1];
            let blue = pixels.data[i + 2]

            const average = (red + green + blue) / 3;
            const luminance = 0.2126 * red +
                0.7152 * green +
                0.0722 * blue;

            red = weightedAverage ? luminance : average;
            green = weightedAverage ? luminance : average;
            blue = weightedAverage ? luminance : average;

            pixels.data[i] = red;
            pixels.data[i + 1] = green;
            pixels.data[i + 2] = blue;
        }
    }
    context
        .putImageData(
            pixels,
            0,
            0,
            0,
            0,
            pixels.width,
            pixels.height
        );
}

Источники

https://www.baeldung.com/cs/convert-rgb-to-grayscale
https://twitter.com/mudasobwa/status/1528046455587495940
https://rosettacode.org/wiki/Grayscale_image

Ссылки

http://papugi.demensdeum.repl.co/

Благодарности

Спасибо Aleksei Matiushkin (https://twitter.com/mudasobwa) за наводку на Rosetta Code

How to Run CSGO on Macbook M1

If you get the SDL_GetDesktopDisplayMode_REAL error on your Macbook M1 when launching CSGO, then do as written below.
1. Add launch options to Steam for CSGO:
-w 1440 -h 900 -fullscreen
2. Launch CSGO via Steam
3. Click Ignore or Always Ignore the SDL_GetDesktopDisplayMode_REAL error
4. Enjoy

Turing Bomb

In 1936, scientist Alan Turing in his publication “On Computable Numbers, With An Application to Entscheidungsproblem” describes the use of a universal computing machine that could put an end to the question of the solvability problem in mathematics. As a result, he comes to the conclusion that such a machine would not be able to solve anything correctly if the result of its work was inverted and looped back to itself. It turns out that it is impossible to create an *ideal* antivirus, an *ideal* tile layer, a program that suggests ideal phrases for your crash, etc. Paradox!

However, this universal computing machine can be used to implement any algorithm, which is what British intelligence took advantage of by hiring Turing and allowing him to create the “Bombe” machine to decipher German messages during World War II.

The following is an OOP simulation of a single-tape computer in Dart, based on the original document.

A Turing machine consists of a film divided into sections, each section contains a symbol, the symbols can be read or written. An example of a film class:

final _map = Map<int, String>(); 

  String read({required int at}) { 
    return _map[at] ?? ""; 
  } 

  void write({required String symbol, required int at}) { 
    _map[at] = symbol; 
  } 
}

There is also a “scanning square”, it can move along the film, read or write information, in modern language – a magnetic head. An example of a magnetic head class:

  int _index = 0; 
  InfiniteTape _infiniteTape; 
  TapeHead(this._infiniteTape) {} 

  String next() { 
    _index += 1; 
    move(to: _index); 
    final output = read(); 
    return output; 
  } 

  String previous() { 
    _index -= 1; 
    move(to: _index); 
    final output = read(); 
    return output; 
  } 

  void move({required int to}) { 
    this._index = to; 
  } 

  String read() { 
    return _infiniteTape.read(at: this._index); 
  } 

  void write(String symbol) { 
    _infiniteTape.write(symbol: symbol, at: this._index); 
  } 

  int index() { 
    return _index; 
  } 
}

The machine contains “m-configurations” by which it can decide what to do next. In modern language, these are states and state handlers. An example of a state handler:

  FiniteStateControlDelegate? delegate = null; 

  void handle({required String symbol}) { 
    if (symbol == OPCODE_PRINT) { 
      final argument = delegate?.nextSymbol(); 
      print(argument);
    } 
    else if (symbol == OPCODE_GENERATE_RANDOM_NUMBER_FROM_ZERO_TO_AND_WRITE_AFTER) { 
      final to = int.tryParse(delegate!.nextSymbol())!; 
      final value = new Random().nextInt(to); 
      delegate!.nextSymbol(); 
      delegate!.write(value.toString()); 
    } 
    else if (symbol == OPCODE_INPUT_TO_NEXT) { 
      final input = stdin.readLineSync()!; 
      delegate?.nextSymbol(); 
      delegate?.write(input); 
    } 
    else if (symbol == OPCODE_COPY_FROM_TO) { 
      final currentIndex = delegate!.index(); 

и т.д.

After this, you need to create “configurations”, in modern language these are operation codes (opcodes), their handlers. An example of opcodes:

const OPCODE_PRINT = "print"; 
const OPCODE_INCREMENT_NEXT = "increment next"; 
const OPCODE_DECREMENT_NEXT = "decrement next"; 
const OPCODE_IF_PREVIOUS_NOT_EQUAL = "if previous not equal"; 
const OPCODE_MOVE_TO_INDEX = "move to index"; 
const OPCODE_COPY_FROM_TO = "copy from index to index"; 
const OPCODE_INPUT_TO_NEXT = "input to next"; 
const OPCODE_GENERATE_RANDOM_NUMBER_FROM_ZERO_TO_AND_WRITE_AFTER = "generate random number from zero to next and write after";

Don’t forget to create an opcode and a stop handler, otherwise you won’t be able to prove or not prove (sic!) the resolution problem.

Now, using the “mediator” pattern, we connect all the classes in the Turing Machine class, create an instance of the class, record the programs on tape using a tape recorder, load the tape and you can use it!

For me personally, the question of what came first remains interesting: the creation of a universal computer or the proof of the “Entscheidungsproblem”, which resulted in the computer appearing as a by-product.

Cassettes

For fun, I recorded several cassette programs for my version of the machine.

Hello World

hello world 
stop

Считаем до 16-ти

0
if previous not equal
16
copy from index to index
1
8
print
?
move to index
0
else
copy from index to index
1
16
print
?
print
Finished!
stop

Самой интересной задачей было написание Quine программы, которая печатает свой исходный код, для одноленточной машины. Первые 8 часов мне казалось что эта задача не решаема с таким малым количеством опкодов, однако всего через 16 часов оказалось что я был не прав.

Реализация и примеры кассет, источники ниже.

Ссылки

https://gitlab.com/demensdeum/turing-machine

Источники

https://www.astro.puc.cl/~rparra/tools/PAPERS/turing_1936.pdf
https://kpolyakov.spb.ru/prog/turing.htm
https://www.youtube.com/watch?v=dNRDvLACg5Q
https://www.youtube.com/watch?v=jP3ceURvIYc
https://www.youtube.com/watch?v=9QCJj5QzETI
https://www.youtube.com/watch?v=HeQX2HjkcNo&t=0s